题目内容
 已知,如图,某人站在斜坡端点C处,距离塔底中心B点100米位置,测得塔顶的仰角为60°,又走到坡度为1:2的斜坡P处测得塔顶A的仰角为45°.
已知,如图,某人站在斜坡端点C处,距离塔底中心B点100米位置,测得塔顶的仰角为60°,又走到坡度为1:2的斜坡P处测得塔顶A的仰角为45°.(1)求塔的高度;
(2)求人在P点时的铅垂高度.
分析:(1)在直角△ABC中,利用三角函数即可求解;
(2)在图中共有三个直角三角形,即Rt△ABC、Rt△AEP、Rt△PCD,利用60°、45°以及坡度比,分别求出AB、AE、PD,然后根据三者之间的关系,列方程求解即可解决.
(2)在图中共有三个直角三角形,即Rt△ABC、Rt△AEP、Rt△PCD,利用60°、45°以及坡度比,分别求出AB、AE、PD,然后根据三者之间的关系,列方程求解即可解决.
解答:解:(1)由题意知:AB⊥BD,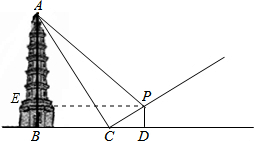
∴∠ABC=90°,
∵∠ACB=60°,BC=100米,
∴AB=BC•tan60°=100
(米);
(2)过P点作PE⊥AB,
可得四边形BDPE为矩形,
在Rt△AEP中,
∵∠APE=45°∴AE=PE
∴AB-BE=BD=BC+CD,
设PD=x,则BE=x,
∵PD:CD=1:2,
∴CD=2x,
∴100
-x=100+2x
解得:x=
,
即人站在P点时的铅垂高度为
米.

∴∠ABC=90°,
∵∠ACB=60°,BC=100米,
∴AB=BC•tan60°=100
| 3 |
(2)过P点作PE⊥AB,
可得四边形BDPE为矩形,
在Rt△AEP中,
∵∠APE=45°∴AE=PE
∴AB-BE=BD=BC+CD,
设PD=x,则BE=x,
∵PD:CD=1:2,
∴CD=2x,
∴100
| 3 |
解得:x=
100(
| ||
| 3 |
即人站在P点时的铅垂高度为
100(
| ||
| 3 |
点评:本题考查了解直角三角形的应用,要求学生借助仰角关系构造直角三角形,并结合图形利用三角函数解直角三角形.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
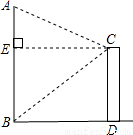
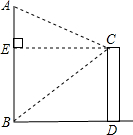
 如图,某人站在楼顶观测对面的笔直的旗杆AB,已知观测点C到对面旗杆的距离(CE的长度)为10m,测得旗杆顶的仰角∠ECA为30°,旗杆底部的俯角∠ECB为45°,那么AB的高度是( )
如图,某人站在楼顶观测对面的笔直的旗杆AB,已知观测点C到对面旗杆的距离(CE的长度)为10m,测得旗杆顶的仰角∠ECA为30°,旗杆底部的俯角∠ECB为45°,那么AB的高度是( )A、(10
| ||||||
B、(10+10
| ||||||
C、(10
| ||||||
D、(10+
|
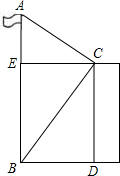
 如图,某人站在楼顶观测对面笔直的旗杆AB,已知观测点C到旗杆的距离(CE的长度)为8米,测得旗杆顶的仰角为∠ECA=30°,旗杆底部的俯角∠ECB=45°,那么旗杆AB的高度是
如图,某人站在楼顶观测对面笔直的旗杆AB,已知观测点C到旗杆的距离(CE的长度)为8米,测得旗杆顶的仰角为∠ECA=30°,旗杆底部的俯角∠ECB=45°,那么旗杆AB的高度是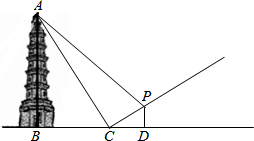 已知,如图,某人站在斜坡端点C处,距离塔底中心B点100米位置,测得塔顶的仰角为60°,又走到坡度为1:2的斜坡P处测得塔顶A的仰角为45°.
已知,如图,某人站在斜坡端点C处,距离塔底中心B点100米位置,测得塔顶的仰角为60°,又走到坡度为1:2的斜坡P处测得塔顶A的仰角为45°.