题目内容
如图所示是一块平行四边形的铁片ABCD,且AB=2AD,现在想用这块铁片截一个直角三角形,并要求斜边与AB重合,面积最大,能否截出符合条件的三角形?如果能截出,画出截线;如果不能截出,说明理由.

解:取CD的中点M,连接AM,BM.
∵AB=CD,AD=BC,AB=2AD,
∴DM=CM= CD,AD=DM,BC=CM.
CD,AD=DM,BC=CM.
∴∠DAM=∠DMA,∠BMC=∠MBC.
∴∠AMD+∠BMC= =180°﹣
=180°﹣ (∠C+∠D).
(∠C+∠D).
∵AD∥BC,
∴∠D+∠C=180°.
∴∠AMD+∠BMC=180°﹣ ×180°=90°,
×180°=90°,
∴∠AMB=180°﹣(∠AMD+∠BMC)=180°﹣90°=90°.
∴AM⊥BM.
∴可截出符合要求的直角三角形. 截法:取CD中点M,连接AM和BM,沿AM,BM剪下即可.
∵AB=CD,AD=BC,AB=2AD,
∴DM=CM=
 CD,AD=DM,BC=CM.
CD,AD=DM,BC=CM.∴∠DAM=∠DMA,∠BMC=∠MBC.
∴∠AMD+∠BMC=
 =180°﹣
=180°﹣ (∠C+∠D).
(∠C+∠D).∵AD∥BC,
∴∠D+∠C=180°.
∴∠AMD+∠BMC=180°﹣
 ×180°=90°,
×180°=90°,∴∠AMB=180°﹣(∠AMD+∠BMC)=180°﹣90°=90°.
∴AM⊥BM.
∴可截出符合要求的直角三角形. 截法:取CD中点M,连接AM和BM,沿AM,BM剪下即可.


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
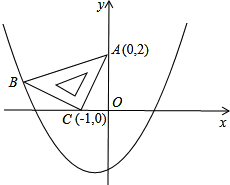 两坐标轴上,且点A(0,2),点C(-1,0),如图所示;抛物线y=ax2+ax-2经过点B.
两坐标轴上,且点A(0,2),点C(-1,0),如图所示;抛物线y=ax2+ax-2经过点B. 表示,有以下四种结论,其中正确的是
表示,有以下四种结论,其中正确的是





 表示,有以下四种结论,其中正确的是
表示,有以下四种结论,其中正确的是





 两坐标轴上,且点A(0,2),点C(-1,0),如图所示;抛物线y=ax2+ax-2经过点B.
两坐标轴上,且点A(0,2),点C(-1,0),如图所示;抛物线y=ax2+ax-2经过点B.