题目内容
）如图，在△ABC中，点D在AB上，且CD=CB，点E为BD的中点，点F为AC的中点，连结EF交CD于点M，连接AM．
（1）求证：EF=AC．
（2）若∠BAC=45°，求线段AM、DM、BC之间的数量关系．
（1）证明：∵CD=CB，点E为BD的中点，
∴CE⊥BD，
∵点F为AC的中点，
∴EF=AC；
（2）解：∵∠BAC=45°，CE⊥BD，
∴△AEC是等腰直角三角形，
∵点F为AC的中点，
∴EF垂直平分AC，
∴AM=CM，
∵CD=CM+DM=AM+CM，CD=CB，
∴BC=AM+DM．
练习册系列答案
相关题目
下列计算中正确的是（ ）
|
| A． |
| B． |
| C． | a6=（a3）2 | D． | b﹣2=﹣b2 |
+
=
=3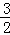
GE，试用含n的式子表示线段AN的长．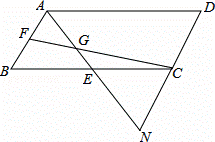
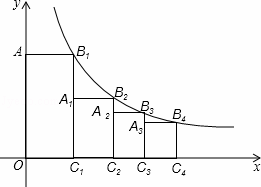
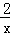（x＞0）的图象上，过点B1分别作x轴和y轴的垂线，垂足为C1和A，点C1的坐标为（1，0）取x轴上一点C2（
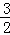，0），过点C2分别作x轴的垂线交反比例函数图象于点B2，过B2作线段B1C1的垂线交B1C1于点A1，依次在x轴上取点C3（2，0），C4（
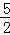，0）…按此规律作矩形，则第n（ n≥2，n为整数）个矩形）An﹣1Cn﹣1CnBn的面积为 ．
如图，在△ABC中，点D、E分别是边AB、AC的中点，∠B=50°，∠A=26°，将△ABC沿DE折叠，点A的对应点是点A′，则∠AEA′的度数是（ ）
|
| A． | 145° | B． | 152° | C． | 158° | D． | 160° |
