题目内容
 如图,△ABC的内切圆⊙O与BC、CA、AB相切于点D、E、F,且AB=9,BC=14,CA=13,则AF=
如图,△ABC的内切圆⊙O与BC、CA、AB相切于点D、E、F,且AB=9,BC=14,CA=13,则AF=4
4
.分析:由切线长定理,可知:AF=AE,CD=CE,BF=BD,用未知数设AF的长,然后表示出BD的长,即可表示出CD的长,根据BD+CD=14,可求出AF的长.
解答:解:设AF=x,
根据切线长定理得AE=x,BD=BF=9-x,CE=CD=CA-AF=13-x,
则有9-x+13-x=14,
解得x=4,
即AF的长为4.
故答案为4.
根据切线长定理得AE=x,BD=BF=9-x,CE=CD=CA-AF=13-x,
则有9-x+13-x=14,
解得x=4,
即AF的长为4.
故答案为4.
点评:此题主要是运用了切线长定理,用已知数和未知数表示所有的切线长,再进一步列方程求解.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
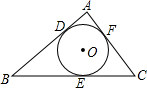 已知如图,△ABC内切⊙O于D、E、F三点,内切圆⊙O的半径为1,∠C=60°,AB=5,则△ABC的周长为( )
已知如图,△ABC内切⊙O于D、E、F三点,内切圆⊙O的半径为1,∠C=60°,AB=5,则△ABC的周长为( )| A、12 | ||
| B、14 | ||
C、10+2
| ||
D、10+
|
 5、已知:如图,△ABC内接于⊙O,AE切⊙O于点A,BD∥AE交AC的延长线于点D,求证:AB2=AC•AD.
5、已知:如图,△ABC内接于⊙O,AE切⊙O于点A,BD∥AE交AC的延长线于点D,求证:AB2=AC•AD.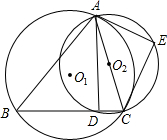 点E,连接AD、CE,若AC=7,AD=3
点E,连接AD、CE,若AC=7,AD=3
