题目内容
己知：如图，⊙O与
内切于点B，BC是⊙O的直径，BC＝6，BF为的直径，BF＝4，⊙O的弦BA交于点D，连接DF、AC、CD．(1)求证：DF∥AC；(2)当∠ABC等于多少度时，CD与相切？并证明你的结论．(3)在(2)的前提下，连接FA交CD于点E，求AF、EF的长．
答案：
解析：
解析：
|
(1)∵BC是⊙O的直径，BF是⊙  的直径，
∴∠ BDF＝∠BAC＝ ，
∴ DF∥AC．(2)当∠ABC＝  时，CD与⊙相切．
连接  ，∵⊙的直径BF＝4，
⊙ O的直径BC＝6，∴ FC＝ ＝2．
在 Rt△BFD中，由BF＝4，∠ABC＝ ．
∴ DF＝2，∴DF＝＝FC＝2．
∴  为直角三角形，
∴  ＝ ．
又∵点 D在⊙上，
∴ CD与⊙相切．
(3)在Rt△ABC中，∠ABC＝  ，BC＝6，∴AC＝3，AB＝3 ．
在 Rt△DBF中，∠ABC＝，BF＝4，
∴ DF＝2，BD＝2 ，∴AD＝ ．
在 Rt△ADF中，AF＝  ＝ ．
∵ DF∥AC，∴ ＝ ＝ ．
∴  ＝ ，
∴ EF＝ AF＝ ．
|
练习册系列答案
相关题目
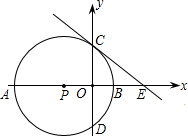D，其中A（-3，0），B（1，0）．过点C作⊙P的切线交x轴于点E．
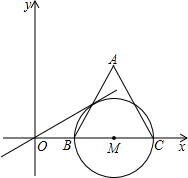点，以BC为直径的⊙M交AB于E．
的费用为20元/平方米，新建（含装修）墙壁的费用为80元/平方米，设健身房高3米，健身房AB的长为x米，BC的长为y米，修建健身房墙壁的总投资为w元．