题目内容
13.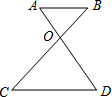 如图AB∥CD,AD、BC交于O点,则下列各式:
如图AB∥CD,AD、BC交于O点,则下列各式:①$\frac{OA}{OD}=\frac{OB}{OC}$
②$\frac{OA}{OB}=\frac{OD}{OC}$
③$\frac{OA}{OD}=\frac{AB}{CD}$
④$\frac{OA}{AD}=\frac{OB}{BC}$
中成立的式子共有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 由AB∥CD,可得△ABE∽△DCE,然后由相似三角形的对应边成比例,求得答案.
解答 解:∵AB∥CD,
∴△ABE∽△DCE,
∴$\frac{OA}{OD}=\frac{OB}{OC},\frac{OA}{OB}=\frac{OD}{OC},\frac{OA}{OD}=\frac{AB}{CD}$,
故选C
点评 此题考查了相似三角形的判定与性质.注意证得△ABE∽△DCE是关键.

练习册系列答案
相关题目
18.若一元二次方程ax2+bx+c=0的一个根为-1,则( )
| A. | a+b+c=0 | B. | a-b+c=0 | C. | -a-b+c=0 | D. | -a+b+c=0 |
5.有六张卡片,上面各写有1,1,2,3,4,4六个数,从中任意摸一张,摸到奇数的概率是( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |
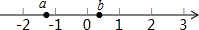 已知a、b在数轴上的位置如图,则a+b,a-b,b-a,-a-b中,最大的数是哪一个?
已知a、b在数轴上的位置如图,则a+b,a-b,b-a,-a-b中,最大的数是哪一个?
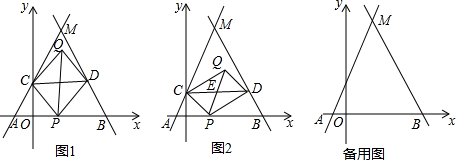
 如图所示,直线y=x+2与x轴交于点A,与y轴交于点B,AB⊥BC,且点C在x轴上,若抛物线y=ax2+bx+c以C为顶点,且经过点B,求这条抛物线的解析式.
如图所示,直线y=x+2与x轴交于点A,与y轴交于点B,AB⊥BC,且点C在x轴上,若抛物线y=ax2+bx+c以C为顶点,且经过点B,求这条抛物线的解析式.