题目内容
14.阅读下列材料:我们知道|x|的几何意义是在数轴上数x对应的点与原点的距离,即|x|=|x-0|.也就是说|x|表示在数轴上数x与数0对应的点之间的距离.这个结论可以推广为|x1-x2|表示在数轴上数x1与x2对应的点之间的距离.请你根据对以上知识的理解解答下列问题.(1)如果|x-2|+|x+1|=3,求x的取值范围;
(2)如果|x-3|+|2+x|>5,求x的取值范围.
分析 (1)如果|x-2|+|x+1|=3,则$\left\{\begin{array}{l}{x-2≤0}\\{x+1≥0}\end{array}\right.$,据此解不等式,求出x的取值范围即可.
(2)首先根据x的取值范围,求出|x-3|+|2+x|的值是多少;然后根据一元一次不等式的求解方法,求出x的取值范围即可.
解答 解:(1)∵|x-2|+|x+1|=3,
∴$\left\{\begin{array}{l}{x-2≤0}\\{x+1≥0}\end{array}\right.$,
解得-1≤x≤2,
即x的取值范围是:-1≤x≤2.
(2)①当x≤-2时,
∵|x-3|+|2+x|>5,
∴-(x-3)-(2+x)>5,
∴-2x+1>5,
解得x<-2;
∴x的取值范围是:x<-2.
②当-2<x<3时,
∵|x-3|+|2+x|>5,
∴-(x-3)+(2+x)>5,
∴5>5,
此题x无解;
③当x≥3时,
∵|x-3|+|2+x|>5,
∴(x-3)+(2+x)>5,
∴2x-1>5,
解得x>3;
综上,可得x的取值范围是:x<-2或x>3.
点评 (1)此题主要考查了绝对值的含义以及求法,考查了分类讨论思想的应用,要熟练掌握,解答此题的关键是要明确:①当a是正有理数时,a的绝对值是它本身a; ②当a是负有理数时,a的绝对值是它的相反数-a; ③当a是零时,a的绝对值是零.即|a|={a(a>0)0(a=0)-a(a<0).
(2)此题还考查了一元一次不等式的求法,要熟练掌握.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
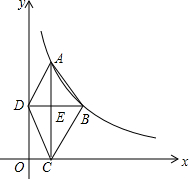 如图所示,反比例函数y=$\frac{k}{x}$(x>0,k>0)的图象经过点A(1,4)和点B(a,b),其中a>1,过点A作x轴的垂线,垂点为C,过点B作y轴的垂线,垂足为D,AC与BD相交于点E,连接AD,DC,CB.
如图所示,反比例函数y=$\frac{k}{x}$(x>0,k>0)的图象经过点A(1,4)和点B(a,b),其中a>1,过点A作x轴的垂线,垂点为C,过点B作y轴的垂线,垂足为D,AC与BD相交于点E,连接AD,DC,CB.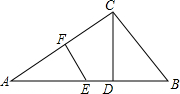 如图,在Rt△ABC中,∠ACB=90°,AF=4,EF⊥AC交AB于E,CD⊥AB,垂足为D.若CD=4,EF=3.则ED=$\frac{1}{3}$,BC=5,AB=$\frac{25}{3}$.
如图,在Rt△ABC中,∠ACB=90°,AF=4,EF⊥AC交AB于E,CD⊥AB,垂足为D.若CD=4,EF=3.则ED=$\frac{1}{3}$,BC=5,AB=$\frac{25}{3}$.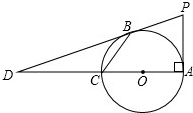 如图所示,AC为⊙O的直径且PA⊥AC,BC是⊙O的一条弦,直线PB交直线AC于点D,且PB=PA.
如图所示,AC为⊙O的直径且PA⊥AC,BC是⊙O的一条弦,直线PB交直线AC于点D,且PB=PA.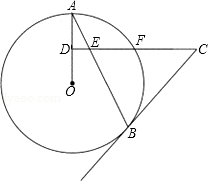 AB是⊙O的弦,D为半径OA的中点,过D作CD⊥OA交弦AB于点E,交⊙O于点F,且CE=CB.
AB是⊙O的弦,D为半径OA的中点,过D作CD⊥OA交弦AB于点E,交⊙O于点F,且CE=CB.