题目内容
 已知|a|=2,|b|=2,|c|=3,且a,b,c在数轴的位置如图所示,计算a-|2b|-3c的值.
已知|a|=2,|b|=2,|c|=3,且a,b,c在数轴的位置如图所示,计算a-|2b|-3c的值.考点:数轴,绝对值
专题:
分析:由数轴可得b<0<a<c,然后由|a|=2,|b|=2,|c|=3,可求a、b、c的值,再把a、b、c的值代入即可.
解答:解:∵|a|=2,|b|=2,|c|=3,
∴a=±2,b=±2,c=±3,
∵由数轴可得b<0<a<c,
∴a=2,b=-2,c=3.
将a=2,b=-2,c=3,代入a-|2b|-3c得:
2-|2×(-2)|-3×3
=2-4-9
=-11.
∴a=±2,b=±2,c=±3,
∵由数轴可得b<0<a<c,
∴a=2,b=-2,c=3.
将a=2,b=-2,c=3,代入a-|2b|-3c得:
2-|2×(-2)|-3×3
=2-4-9
=-11.
点评:此题考查了数轴及绝对值的有关知识,解题的关键是结合数轴确定a、b、c的值.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
 二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出下列四个结论:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出下列四个结论:①4ac-b2<0;②当x<-2时,y随x的减小而减小;③c<0;④b=2a,其中正确结论的个数是( )
| A、4个 | B、3个 | C、2个 | D、1个 |
 将三角形绕直线l旋转一周,可以得到如图所示的立体图形的是( )
将三角形绕直线l旋转一周,可以得到如图所示的立体图形的是( )A、 |
B、 |
C、 |
D、 |
若
=0,则a的值为( )
| |a|-5 |
| a-5 |
| A、0 | B、5 | C、-5 | D、±5 |
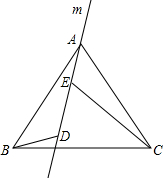 如图,直线m经过正三角形ABC的顶点A,在直线m上取两点D,E,使得使∠ADB=∠AEC=120°.通过观察或测量,猜想线段BD,CE与DE之间满足的数量关系,并予以证明.
如图,直线m经过正三角形ABC的顶点A,在直线m上取两点D,E,使得使∠ADB=∠AEC=120°.通过观察或测量,猜想线段BD,CE与DE之间满足的数量关系,并予以证明.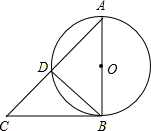 如图,AB是⊙O的直径,AD是⊙O的弦,过点B的切线交AD的延长线于点C.若AD=DC,求∠ABD的度数.
如图,AB是⊙O的直径,AD是⊙O的弦,过点B的切线交AD的延长线于点C.若AD=DC,求∠ABD的度数. 如图,在5×5的正方形网络,在网格中画出点F,使得△DEF与△ABC全等,这样的格点三角最多可以画出
如图,在5×5的正方形网络,在网格中画出点F,使得△DEF与△ABC全等,这样的格点三角最多可以画出