题目内容
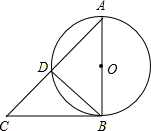 如图,AB是⊙O的直径,AD是⊙O的弦,过点B的切线交AD的延长线于点C.若AD=DC,求∠ABD的度数.
如图,AB是⊙O的直径,AD是⊙O的弦,过点B的切线交AD的延长线于点C.若AD=DC,求∠ABD的度数.考点:切线的性质
专题:计算题
分析:先根据切线的性质,由BC为⊙O的切线得到∠ABC=90°,再根据圆周角定理,由AB是⊙O的直径得到∠ADB=90°,则BD⊥AC,加上AD=CD,根据等腰三角形的判定可得△ABC为等腰直角三角形,然后根据等腰三角形的性质易得∠ABD=
∠ABC=45°.
| 1 |
| 2 |
解答:解:∵BC为⊙O的切线,
∴AB⊥BC,
∴∠ABC=90°,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴BD⊥AC,
而AD=CD,
∴△ABC为等腰直角三角形,
∴BD平分∠ABC,
∴∠ABD=45°.
∴AB⊥BC,
∴∠ABC=90°,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴BD⊥AC,
而AD=CD,
∴△ABC为等腰直角三角形,
∴BD平分∠ABC,
∴∠ABD=45°.
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了圆周角定理和等腰三角形的判定与性质.

练习册系列答案
相关题目
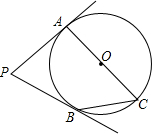 如图,PA、PB是⊙O的两条切线,A、B为切点,AC为⊙O的直径,∠P=70°,则∠PBC=( )
如图,PA、PB是⊙O的两条切线,A、B为切点,AC为⊙O的直径,∠P=70°,则∠PBC=( )| A、110° | B、120° |
| C、135° | D、145° |
下列分式变形正确的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列函数不是反比例函数的是( )
| A、y=3x-1 | ||
B、y=-
| ||
| C、xy=5 | ||
D、y=
|
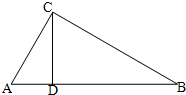 如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的高,AB=13cm,BC=12cm,AC=5cm.(1)求△ABC的面积;(2)求CD的长.
如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的高,AB=13cm,BC=12cm,AC=5cm.(1)求△ABC的面积;(2)求CD的长.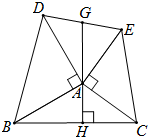 如图,AB=AD,AC=AE,∠BAD=∠CAE=90°.AH⊥BC于点H,HA的延长线交DE于G.求证:GD=GE.
如图,AB=AD,AC=AE,∠BAD=∠CAE=90°.AH⊥BC于点H,HA的延长线交DE于G.求证:GD=GE. 已知|a|=2,|b|=2,|c|=3,且a,b,c在数轴的位置如图所示,计算a-|2b|-3c的值.
已知|a|=2,|b|=2,|c|=3,且a,b,c在数轴的位置如图所示,计算a-|2b|-3c的值.