题目内容
 如图,AB∥CD,BE=CF,若使△DCF≌△ABE,还需添加一个条件是(写一个答案即可)
如图,AB∥CD,BE=CF,若使△DCF≌△ABE,还需添加一个条件是(写一个答案即可)考点:全等三角形的判定
专题:开放型
分析:根据平行线的性质求出∠B=∠C,根据SAS推出即可,此题是一道开放型的题目,答案不唯一.
解答:解:AB=CD,
理由是:∵AB∥CD,
∴∠B=∠C,
在△DCF和△ABE中
∴△DCF≌△ABE,
故答案为:AB=CD.
理由是:∵AB∥CD,
∴∠B=∠C,
在△DCF和△ABE中
|
∴△DCF≌△ABE,
故答案为:AB=CD.
点评:本题考查了全等三角形的判定和平行线的性质的应用,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS.

练习册系列答案
相关题目
如图,已知△ABC的六个元素,则下面甲、乙、丙三个三角形中和△ABC全等的图形是( )

| A、甲和乙 | B、乙和丙 |
| C、只有乙 | D、只有丙 |
若关于x的不等式
的整数解共有4个,则m的取值范围是( )
|
| A、6<m<7 |
| B、6≤m<7 |
| C、6≤m≤7 |
| D、6<m≤7 |
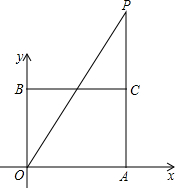 如图,长方形AOBC在直角坐标系中,A、B两点坐标分别为(8,0)、(0,6),点P是长方形一边所在直线上的一个动点,并且它位于y轴右侧.
如图,长方形AOBC在直角坐标系中,A、B两点坐标分别为(8,0)、(0,6),点P是长方形一边所在直线上的一个动点,并且它位于y轴右侧.
 如图,在平面直角坐标系中,若每一个方格的边长代表一个单位.
如图,在平面直角坐标系中,若每一个方格的边长代表一个单位. 如图网格中有△ABC及线段DE,在网格上找一点F(必须在网格的交点处),使△DEF与△ABC全等,这样的点有几个?请画出这些三角形.
如图网格中有△ABC及线段DE,在网格上找一点F(必须在网格的交点处),使△DEF与△ABC全等,这样的点有几个?请画出这些三角形.