题目内容
6．已知k＞0，且关于x的方程3kx2+12x+k+1=0有两个相等的实数根，那么k的值等于3．分析 若一元二次方程有两个相等的实数根，则根的判别式△=b2-4ac=0，据此可列出关于k的等量关系式，即可求得k的值．
解答 解：∵关于x的方程3kx2+12x+k+1=0有两个相等的实数根，
∴△=b2-4ac=144-4×3k×（k+1）=0，
解得k=-4或3，
∵k＞0，
∴k=3．
故答案为3．
点评 本题考查了根的判别式，一元二次方程ax2+bx+c=0（a≠0）的根与△=b2-4ac有如下关系：
（1）△＞0?方程有两个不相等的实数根；
（2）△=0?方程有两个相等的实数根；
（3）△＜0?方程没有实数根．
练习册系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
如图，已知点A在反比例函数y=$\frac{k}{x}$（x＜0）上，作Rt△ABC，点D为斜边AC的中点，连DB并延长交y轴于点E．若△BCE的面积为8，则k=16．
阅读与计算：请阅读以下材料，并完成相应的任务．
14．下列运算正确的是（ ）
| A． | 4m-m=3 | B． | 2m2•m3=2m5 | C． | （-m3）2=m9 | D． | -（m+2n）=-m+2n |
11．下列说法正确的是（ ）
| A． | 1的相反数是-1 | B． | 1的倒数是-1 | C． | 1的立方根是±1 | D． | -1是无理数 |
18．
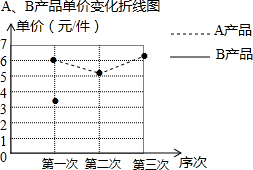某厂生产A，B两种产品，其单价随市场变化而做相应调整．营销人员根据前三次单价变化的情况，绘制了如表统计表及不完整的折线图．
A，B产品单价变化统计表
并求得了A产品三次单价的平均数和方差：
$\overline{{x}_{A}}$=5.9，sA2=$\frac{1}{3}$[（6-5.9）2+（5.2-5.9）2+（6.5-5.9）2]=$\frac{43}{150}$
（1）补全如图中B产品单价变化的折线图．B产品第三次的单价比上一次的单价降低了25%
（2）求B产品三次单价的方差，并比较哪种产品的单价波动小；
（3）该厂决定第四次调价，A产品的单价仍为6.5元/件，B产品的单价比3元/件上调m%（m＞0），使得A产品这四次单价的中位数是B产品四次单价中位数的2倍少1，求m的值．
某厂生产A，B两种产品，其单价随市场变化而做相应调整．营销人员根据前三次单价变化的情况，绘制了如表统计表及不完整的折线图．A，B产品单价变化统计表
| 第一次 | 第二次 | 第三次 | |
| A产品单价（元/件） | 6 | 5.2 | 6.5 |
| B产品单价（元/件） | 3.5 | 4 | 3 |
$\overline{{x}_{A}}$=5.9，sA2=$\frac{1}{3}$[（6-5.9）2+（5.2-5.9）2+（6.5-5.9）2]=$\frac{43}{150}$
（1）补全如图中B产品单价变化的折线图．B产品第三次的单价比上一次的单价降低了25%
（2）求B产品三次单价的方差，并比较哪种产品的单价波动小；
（3）该厂决定第四次调价，A产品的单价仍为6.5元/件，B产品的单价比3元/件上调m%（m＞0），使得A产品这四次单价的中位数是B产品四次单价中位数的2倍少1，求m的值．
15．已知一个单项式的系数是2，次数是3，则这个单项式可以是（ ）
| A． | -2xy2 | B． | 3x2 | C． | 2xy3 | D． | 2x3 |
