Question

19． 为美化校园，学校决定将花园边墙上的矩形门ABCD改为以AC为直径的圆弧形门，如图所示，量得矩形门宽为1m，对角线AC的长为2m，则要打掉墙体的面积为$\frac{5π}{6}$-$\frac{3\sqrt{3}}{4}$m²．

Answer 1

分析 要打掉墙体的面积是圆的面积减矩形面积减弓形BC的面积．

解答 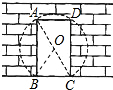解：在Rt△ABC中，
∵AC=2m，BC=1m．
∴∠BAC=30°，BC=1m，AB=$\sqrt{3}$m．
∴∠BCO=60°，即△OBC是等边三角形．
∠BOC所对的弧与弦BC所围成的弓形的面积S₁=$\frac{60π×{1}^{2}}{360}$-$\frac{\sqrt{3}×{1}^{2}}{4}$=$\frac{π}{6}$-$\frac{\sqrt{3}}{4}$（m²）．
∴要打掉的墙体的面积=S_圆O-S_矩形ABCD-S₁=π--$\sqrt{3}$（$\frac{π}{6}$-$\frac{\sqrt{3}}{4}$）=$\frac{5π}{6}$-$\frac{3\sqrt{3}}{4}$．

点评 本题的关键是理解阴影部分的面积是由哪几部分图形组成的，然后利用公式求值．