题目内容
18.若菱形的边长为6,一个内角60°,则菱形较短的对角线长是6,这个菱形面积是18$\sqrt{3}$.分析 证出△ABC是等边三角形,得出AC=AB=6,AO=3,再根据三角函数求出BO,得出BD,菱形的面积等于对角线乘积的一半,即可得出结果.
解答 解:如图所示,连接AC、BD交于点O,
∵菱形的边长为6,一个内角为60°,
∴△ABC是等边三角形,
∴AC=AB=6,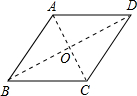
∴这个菱形的较短的对角线长是6,
∵AO=$\frac{1}{2}$AC=3,A0⊥B0.∠ABO=30°,
∴BO=$\frac{AO}{tan30°}$=$\frac{3}{\frac{\sqrt{3}}{3}}$=3$\sqrt{3}$,
∴BD=6$\sqrt{3}$,S菱形ABCD=$\frac{1}{2}$AC×BD=$\frac{1}{2}$×6×6$\sqrt{3}$=18$\sqrt{3}$.
故答案为:6,18$\sqrt{3}$.
点评 本题考查了菱形的对角线互相垂直且平分的性质、三角函数、等边三角形的判定与性质;判断出较短的对角线与两邻边够成等边三角形是解题的关键.

练习册系列答案
相关题目
 如图,在△ABC中,∠C=90°,BC=40,AD是∠BAC的平分线交BC于D,DE⊥AB,且DE:DB=3:5,则DB的长为25.
如图,在△ABC中,∠C=90°,BC=40,AD是∠BAC的平分线交BC于D,DE⊥AB,且DE:DB=3:5,则DB的长为25.
 如图,在平面直角坐标系中,点A(10,0),以OA为直径在第一象限内作半圆C,点B是该半圆周上的一动点,连结OB、AB,并延长AB至点D,使DB=AB,过点D作x轴垂线,分别交x轴.直线OB于点E、F,点E为垂足,连结CF.
如图,在平面直角坐标系中,点A(10,0),以OA为直径在第一象限内作半圆C,点B是该半圆周上的一动点,连结OB、AB,并延长AB至点D,使DB=AB,过点D作x轴垂线,分别交x轴.直线OB于点E、F,点E为垂足,连结CF. 如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,-3)点,点P是直线BC下方的抛物线上一动点.
如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,-3)点,点P是直线BC下方的抛物线上一动点.