题目内容
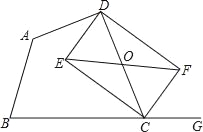
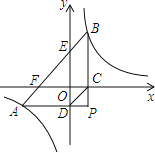
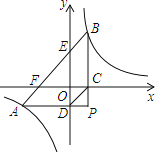
【题目】如图，
的直角顶点P在第四象限，顶点A、B分别落在反比例函数
图象的两支上，且
轴于点C，
轴于点D，AB分别与x轴，y轴相交于点F和
已知点B的坐标为
．
填空：
______；
证明：
；
当四边形ABCD的面积和
的面积相等时，求点P的坐标．
【答案】（1）3；（2）证明见解析；（3）
点坐标为
．
【解析】
由点B的坐标，利用反比例函数图象上点的坐标特征可求出k值；
设A点坐标为
，则D点坐标为
，P点坐标为
，C点坐标为
，进而可得出PB，PC，PA，PD的长度，由四条线段的长度可得出
，结合
可得出
∽
，由相似三角形的性质可得出
，再利用“同位角相等，两直线平行”可证出
；
由四边形ABCD的面积和
的面积相等可得出
，利用三角形的面积公式可得出关于a的方程，解之取其负值，再将其代入P点的坐标中即可求出结论．
解：
点
在反比例函数
的图象，
．
故答案为：3．
证明：
反比例函数解析式为
，
设A点坐标为
轴于点C，
轴于点D，
点坐标为，P点坐标为，C点坐标为，
，
，
，
，
，
，
．
又
，
∽，
，
．
解：四边形ABCD的面积和的面积相等，
，
，
整理得：
，
解得：
，
舍去
，
点坐标为
．
练习册系列答案
新思维寒假作业系列答案
相关题目
