题目内容
13.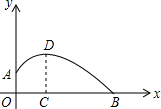 如图所示,某运动员推铅球时,铅球在点A处出手,出手时球离地面约1.8m,出手后铅球在运动过程中,距运动员前3m处(即OC=3m)达到最高点,此时铅球距地面3m,并且铅球经过的路线是抛物线,该运动员的成绩是多少?(精确到0.1m,$\sqrt{10}$取3.2)
如图所示,某运动员推铅球时,铅球在点A处出手,出手时球离地面约1.8m,出手后铅球在运动过程中,距运动员前3m处(即OC=3m)达到最高点,此时铅球距地面3m,并且铅球经过的路线是抛物线,该运动员的成绩是多少?(精确到0.1m,$\sqrt{10}$取3.2)
分析 根据题意首先得出二次函数解析式,进而求出y=0时x的值,进而得出答案.
解答 解:由题意可得:A(0,1.8),D(3,3),
设二次函数的解析式为:y=a(x-3)2+3,
则1.8=a(0-3)2+3,
解得:a=-$\frac{2}{15}$,
故抛物线解析式为:y=-$\frac{2}{15}$(x-3)2+3,
当y=0时,0=-$\frac{2}{15}$(x-3)2+3,
解得:x1=3+$\frac{3\sqrt{10}}{2}$≈7.8,x2=3-$\frac{3\sqrt{10}}{2}$≈-1.8(不合题意舍去),
答:该运动员的成绩是7.8m.
点评 此题主要考查了二次函数的应用,正确求出二次函数解析式是解题关键.

练习册系列答案
相关题目
5.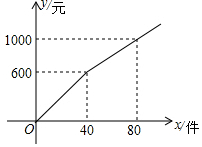 某商店销售一种商品,售出部分商品后进行了降价促销,销售金额y(元)与销售量(x)的函数关系如图所示,则降价后每件商品的销售价格为( )
某商店销售一种商品,售出部分商品后进行了降价促销,销售金额y(元)与销售量(x)的函数关系如图所示,则降价后每件商品的销售价格为( )
 某商店销售一种商品,售出部分商品后进行了降价促销,销售金额y(元)与销售量(x)的函数关系如图所示,则降价后每件商品的销售价格为( )
某商店销售一种商品,售出部分商品后进行了降价促销,销售金额y(元)与销售量(x)的函数关系如图所示,则降价后每件商品的销售价格为( )| A. | 5元 | B. | 10元 | C. | 12.5元 | D. | 15元 |
3.下列各图中,∠1和∠2是对顶角的是( )
| A. |  | B. |  | C. |  | D. |  |
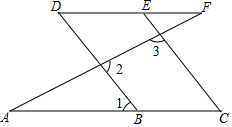 完成推理填空:
完成推理填空: