ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ»γΆΦΘ§≈ΉΈοœΏ![]() ΒΡΆΦœσ”κ
ΒΡΆΦœσ”κ![]() ÷αΫΜ”Ύ
÷αΫΜ”Ύ![]() ΝΫΒψ(Βψ
ΝΫΒψ(Βψ![]() ‘ΎΒψ
‘ΎΒψ![]() ΒΡΉσ±Ώ)”κ
ΒΡΉσ±Ώ)”κ![]() ÷αΫΜ”ΎΒψ
÷αΫΜ”ΎΒψ![]() ,≈ΉΈοœΏΒΡΕΞΒψΈΣ
,≈ΉΈοœΏΒΡΕΞΒψΈΣ![]() .
.
(1)«σΒψ![]() ΒΡΉχ±ξΘΜ
ΒΡΉχ±ξΘΜ
(2)Βψ![]() ΈΣœΏΕΈ
ΈΣœΏΕΈ![]() …œ“ΜΒψ(Βψ
…œ“ΜΒψ(Βψ![]() ≤Μ”κΒψ
≤Μ”κΒψ![]() ÷ΊΚœ)Θ§ΙΐΒψ
÷ΊΚœ)Θ§ΙΐΒψ![]() Ής
Ής![]() ÷αΒΡ¥ΙœΏΘ§”κ÷±œΏ
÷αΒΡ¥ΙœΏΘ§”κ÷±œΏ![]() ΫΜ”ΎΒψ
ΫΜ”ΎΒψ![]() Θ§”κ≈ΉΈοœΏΫΜ”ΎΒψ
Θ§”κ≈ΉΈοœΏΫΜ”ΎΒψ![]() Θ§ΙΐΒψ
Θ§ΙΐΒψ![]() Ής
Ής![]() ΫΜ≈ΉΈοœΏ”ΎΒψ
ΫΜ≈ΉΈοœΏ”ΎΒψ![]() Θ§ΙΐΒψ
Θ§ΙΐΒψ![]() Ής
Ής![]() ÷α”ΎΒψ
÷α”ΎΒψ![]() ,Ω…ΒΟΨΊ–Έ
,Ω…ΒΟΨΊ–Έ![]() .»γΆΦΘ§Βψ
.»γΆΦΘ§Βψ![]() ‘ΎΒψ
‘ΎΒψ![]() Ήσ±ΏΘ§Β±ΨΊ–Έ
Ήσ±ΏΘ§Β±ΨΊ–Έ![]() ΒΡ÷ή≥ΛΉν¥σ ±Θ§«σ¥Υ ±ΒΡ
ΒΡ÷ή≥ΛΉν¥σ ±Θ§«σ¥Υ ±ΒΡ![]() ΒΡΟφΜΐΘΜ
ΒΡΟφΜΐΘΜ
(3)‘Ύ(2)ΒΡΧθΦΰœ¬Θ§Β±ΨΊ–Έ![]() ΒΡ÷ή≥ΛΉν¥σ ±Θ§Ν§Ϋ”
ΒΡ÷ή≥ΛΉν¥σ ±Θ§Ν§Ϋ”![]() Θ§Ιΐ≈ΉΈοœΏ…œ“ΜΒψ
Θ§Ιΐ≈ΉΈοœΏ…œ“ΜΒψ![]() Ής
Ής![]() ÷αΒΡΤΫ––œΏΘ§”κ÷±œΏ
÷αΒΡΤΫ––œΏΘ§”κ÷±œΏ![]() ΫΜ”ΎΒψ
ΫΜ”ΎΒψ![]() (Βψ
(Βψ![]() ‘ΎΒψ
‘ΎΒψ![]() ΒΡ…œΖΫ)»τ
ΒΡ…œΖΫ)»τ![]() Θ§«σΒψ
Θ§«σΒψ![]() ΒΡΉχ±ξ.
ΒΡΉχ±ξ.

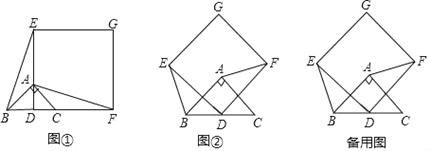
ΓΨ¥πΑΗΓΩ(1)![]() Θ§
Θ§ ![]() Θ§
Θ§![]() ΘΜ(2)
ΘΜ(2)![]() ΘΜ(3)
ΘΜ(3)![]() Μρ
Μρ![]() .
.
ΓΨΫβΈωΓΩ
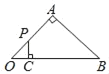
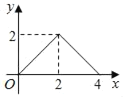
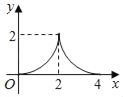
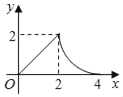
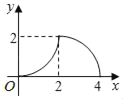
Θ®1Θ©Νν![]() Θ§Ω…«σ≥ωAΓΔBΝΫΒψΉχ±ξΘ§Ννx=0Θ§Ω…«σ≥ωΒψCΒΡΉχ±ξΘΜΘ®2Θ©«σΨΊ–ΈΒΡΟφΜΐΚ· ΐΫβΈω ΫΘ§Ά®ΙΐΕΞΒψΉχ±ξ«σ≥ωm,‘Ό«σ÷±œΏ
Θ§Ω…«σ≥ωAΓΔBΝΫΒψΉχ±ξΘ§Ννx=0Θ§Ω…«σ≥ωΒψCΒΡΉχ±ξΘΜΘ®2Θ©«σΨΊ–ΈΒΡΟφΜΐΚ· ΐΫβΈω ΫΘ§Ά®ΙΐΕΞΒψΉχ±ξ«σ≥ωm,‘Ό«σ÷±œΏ![]() ΒΡΫβΈω ΫΘ§«σ≥ω
ΒΡΫβΈω ΫΘ§«σ≥ω![]() Θ§
Θ§![]() Θ§Ι
Θ§Ι ![]() ΘΜΘ®3Θ©÷Λ
ΘΜΘ®3Θ©÷Λ![]() ”κ‘≠Βψ÷ΊΚœΘ§
”κ‘≠Βψ÷ΊΚœΘ§![]() Βψ”κ
Βψ”κ![]() Βψ÷ΊΚœΘ§Ι
Βψ÷ΊΚœΘ§Ι ![]() Θ§Α―
Θ§Α―![]() ¥ζ»κ
¥ζ»κ![]() Θ§ΫβΒΟ
Θ§ΫβΒΟ![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() ΘΜ…η
ΘΜ…η![]() Θ§‘ρ
Θ§‘ρ![]() Θ§ΒΟ
Θ§ΒΟ![]() .ΫβΒΟ
.ΫβΒΟ![]() Μρ
Μρ![]() Θ§Ω…ΒΟFΉχ±ξ.
Θ§Ω…ΒΟFΉχ±ξ.
”…≈ΉΈοœΏ![]() Ω…÷ΣΘ§
Ω…÷ΣΘ§![]() .
.
Νν![]() Θ§‘ρ
Θ§‘ρ![]() Θ§
Θ§
ΫβΒΟΘ§![]() Μρ
Μρ![]() Θ§
Θ§![]() Θ§
Θ§![]()
(2)”…≈ΉΈοœΏ![]() Ω…÷ΣΘ§Ε‘≥Τ÷αΈΣ
Ω…÷ΣΘ§Ε‘≥Τ÷αΈΣ![]() .
.
![]() Θ§PΘ®m,
Θ§PΘ®m,![]() Θ©,N(-2-m,0)
Θ©,N(-2-m,0)
![]() Θ§
Θ§![]() Θ§
Θ§
![]() ΨΊ–Έ
ΨΊ–Έ![]() ΒΡ÷ή≥Λ
ΒΡ÷ή≥Λ![]()
![]()
![]() Θ§
Θ§
![]() ΨΊ–ΈΒΡ÷ή≥ΛΉν¥σ ±Θ§
ΨΊ–ΈΒΡ÷ή≥ΛΉν¥σ ±Θ§![]() .
.
![]() Θ§
Θ§![]() …η÷±œΏ
…η÷±œΏ![]() ΒΡΫβΈω Ϋ
ΒΡΫβΈω Ϋ![]() Θ§
Θ§![]()
ΫβΒΟ![]() Θ§
Θ§![]() Θ§
Θ§![]() ΫβΈω Ϋ
ΫβΈω Ϋ![]() Θ§Νν
Θ§Νν![]() Θ§‘ρ
Θ§‘ρ![]() Θ§
Θ§
![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§
![]() .
.
(3)![]() Θ§≈ΉΈοœΏΒΡΕ‘≥Τ÷αΈΣ
Θ§≈ΉΈοœΏΒΡΕ‘≥Τ÷αΈΣ![]() Θ§
Θ§
![]() ”Π”κ‘≠Βψ÷ΊΚœΘ§
”Π”κ‘≠Βψ÷ΊΚœΘ§![]() Βψ”κ
Βψ”κ![]() Βψ÷ΊΚœΘ§
Βψ÷ΊΚœΘ§
![]() Θ§Α―
Θ§Α―![]() ¥ζ»κ
¥ζ»κ![]() Θ§ΫβΒΟ
Θ§ΫβΒΟ![]() Θ§
Θ§
![]() Θ§
Θ§![]() .
.
![]() Θ§
Θ§
![]()
…η![]() Θ§‘ρ
Θ§‘ρ![]() Θ§
Θ§![]() Βψ
Βψ![]() ‘ΎΒψ
‘ΎΒψ![]() ΒΡ…œΖΫ«“
ΒΡ…œΖΫ«“![]() Θ§
Θ§
![]() .ΫβΒΟ
.ΫβΒΟ![]() Μρ
Μρ![]() Θ§
Θ§
![]() Μρ
Μρ![]() .
.

 “ΜœΏΟϊ ΠΧα”≈ ‘ΨμœΒΝ–¥πΑΗ
“ΜœΏΟϊ ΠΧα”≈ ‘ΨμœΒΝ–¥πΑΗ