题目内容
18.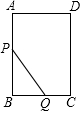 如图,在矩形ABCD中,AB=4cm,BC=3cm,动点P从点A出发,沿AB以1cm/s的速度向终点B匀速运动,同时点Q从点B出发,沿B→C→D以1cm/s的速度向终点D匀速运动,当两个点中有一个到达终点后,另一个点也随之停止.连接PQ,设点P的运动时间为x(s),PQ2=y(cm2).
如图,在矩形ABCD中,AB=4cm,BC=3cm,动点P从点A出发,沿AB以1cm/s的速度向终点B匀速运动,同时点Q从点B出发,沿B→C→D以1cm/s的速度向终点D匀速运动,当两个点中有一个到达终点后,另一个点也随之停止.连接PQ,设点P的运动时间为x(s),PQ2=y(cm2).(1)当点Q在边CD上,且PQ=3时,求x的值;
(2)求y与x之间的函数关系式,并写出自变量x的取值范围;
(3)直接写出y随x增大而增大时自变量x的取值范围.
分析 (1)根据条件可知四边形PBCQ是矩形,推出PB=CQ,列出方程即可解决问题.
(2)分两种情形①如图②中,当0≤x≤3时,②如图③中,当3<x≤4时,过点Q作QE⊥AB于点E,分别利用勾股定理即可解决问题.
(3)把(2)中的二次函数,利用配方法,求出对称轴,即可判断.
解答 解:(1)如图①中,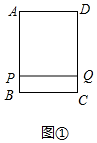
当点Q在边CD上时,且PQ=AD=3,则PQ∥BC,四边形PBCQ是矩形,
∴PB=CQ,
∴4-x=x-3,
∴x=3.5.
(2)如图②中,
当0≤x≤3时,y=(4-x)2+x2=2x2-8x+16.
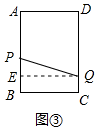
如图③中,当3<x≤4时,过点Q作QE⊥AB于点E,则QE=3,
y=(7-2x)2+32=4x2-28x+58.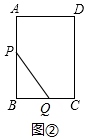
(3)∵当0≤x≤3时,y=2x2-8x+16=2(x-2)2+8.
当3<x≤4时,y=4x2-28x+58=4(x-$\frac{7}{2}$)2+9.
∴当2≤x≤3或$\frac{7}{2}$$≤\\;x$x≤4时,y随x增大而增大.
点评 本题考查二次函数综合题、勾股定理.二次函数的增减性等知识,解题的关键是理解题意,学会分类讨论,灵活应用配方法确定对称轴位置,利用二次函数的增减性解决问题,属于中考常考题型.

练习册系列答案
相关题目
8.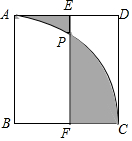 如图,在边长为2的正方形ABCD中,以B点为圆心,AB为半径构造扇形ABC,点P是AC上一动点,过P作EF⊥BC,分别交AD、BC于E、F.记AE、PE、$\widehat{AP}$构成的封闭区域为S1,PF、FC、$\widehat{PC}$构成的封闭区域为S2,当S1与S2面积相等时,BF的长为( )
如图,在边长为2的正方形ABCD中,以B点为圆心,AB为半径构造扇形ABC,点P是AC上一动点,过P作EF⊥BC,分别交AD、BC于E、F.记AE、PE、$\widehat{AP}$构成的封闭区域为S1,PF、FC、$\widehat{PC}$构成的封闭区域为S2,当S1与S2面积相等时,BF的长为( )
 如图,在边长为2的正方形ABCD中,以B点为圆心,AB为半径构造扇形ABC,点P是AC上一动点,过P作EF⊥BC,分别交AD、BC于E、F.记AE、PE、$\widehat{AP}$构成的封闭区域为S1,PF、FC、$\widehat{PC}$构成的封闭区域为S2,当S1与S2面积相等时,BF的长为( )
如图,在边长为2的正方形ABCD中,以B点为圆心,AB为半径构造扇形ABC,点P是AC上一动点,过P作EF⊥BC,分别交AD、BC于E、F.记AE、PE、$\widehat{AP}$构成的封闭区域为S1,PF、FC、$\widehat{PC}$构成的封闭区域为S2,当S1与S2面积相等时,BF的长为( )| A. | 1 | B. | $\frac{4}{3}$ | C. | $\sqrt{2}$ | D. | $\frac{π}{2}$ |
 如图,在⊙O中,$\widehat{AC}$=$\widehat{BC}$,OD=$\frac{1}{2}$AO,OE=$\frac{1}{2}$OB,求证:CD=CE.
如图,在⊙O中,$\widehat{AC}$=$\widehat{BC}$,OD=$\frac{1}{2}$AO,OE=$\frac{1}{2}$OB,求证:CD=CE.
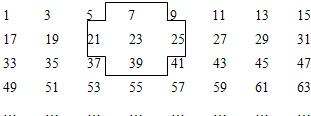 将连续的奇数1、3、5、7、9、…排成如图的数表:
将连续的奇数1、3、5、7、9、…排成如图的数表: