Question

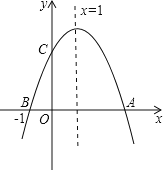
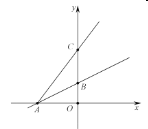
【题目】如图，在平面直角坐标系中，直线与轴、轴分别交于点、，点是轴正半轴上的一点，当时，则点的纵坐标是（ ）

A.2B.C.D.

Answer 1

【答案】D

【解析】

首先过点B作BD⊥AC于点D，设BC=a，根据直线解析式得到点A、B坐标，从而求出OA 、OB的长，易证△BCD ≌△ACO，再根据相似三角形的对应边成比例得出比例式，即可解答.

解：过点B作BD⊥AC于点D，设BC=a，

∵直线与轴、轴分别交于点、，

∴A(-2,0)，B（0,1），即OA=2， OB=1，AC=，

∵，

∴AB平分∠CAB，

又∵BO⊥AO，BD⊥AC，

∴BO= BD=1，

∵∠BCD =∠ACO，∠CDB=∠COA =90°，

∴△BCD ≌△ACO，

∴ ，即a:=1:2

解得：a1=， a2=-1（舍去），

∴OC=OB+BC=+1=，所以点C的纵坐标是.

故选：D.