题目内容
二次函数y=ax2+bx+c(a,b,c是常数,a≠0),下列说法:
①若b2-4ac=0,则抛物线的顶点一定在x轴上;
②若b=a+c,则抛物线必经过点(-1,0);
③若a<0,且一元二次方程ax2+bx+c=0有两根x1,x2(x1<x2),则ax2+bx+c<0的解集为x1<x<x2;
④若b=3a+
,则方程ax2+bx+c=0有一根为-3.
其中正确的是 (把正确说法的序号都填上).
①若b2-4ac=0,则抛物线的顶点一定在x轴上;
②若b=a+c,则抛物线必经过点(-1,0);
③若a<0,且一元二次方程ax2+bx+c=0有两根x1,x2(x1<x2),则ax2+bx+c<0的解集为x1<x<x2;
④若b=3a+
| c |
| 3 |
其中正确的是
考点:二次函数的性质
专题:代数综合题
分析:令y=0,利用根的判别式判定顶点在x轴上,令x=-1求出a、b、c的关系式,判断②正确;a<0时,抛物线开口向下,根据二次函数的增减性写出不等式的解集,判断③错误;把已知等式整理得到a、b、c的关系式,然后判断出x=-3,从而得到④正确.
解答:解:令y=0,则ax2+bx+c=0,
∵b2-4ac=0,
∴抛物线与x轴只有一个交点,即顶点一定在x轴上,故①正确;
x=-1时,a-b+c=0,
∴b=a+c,
∴b=a+c,则抛物线必经过点(-1,0)正确,故②正确;
a<0时,二次函数y=ax2+bx+c图象开口向下,
ax2+bx+c<0的解集为x<x1或x>x2,故③错误;
∵b=3a+
,
∴9a-3b+c=0,
∴a(-3)2+b(-3)+c=0,
∴方程ax2+bx+c=0有一根为-3,故④正确.
综上所述,正确的是①②④.
故答案为:①②④.
∵b2-4ac=0,
∴抛物线与x轴只有一个交点,即顶点一定在x轴上,故①正确;
x=-1时,a-b+c=0,
∴b=a+c,
∴b=a+c,则抛物线必经过点(-1,0)正确,故②正确;
a<0时,二次函数y=ax2+bx+c图象开口向下,
ax2+bx+c<0的解集为x<x1或x>x2,故③错误;
∵b=3a+
| c |
| 3 |
∴9a-3b+c=0,
∴a(-3)2+b(-3)+c=0,
∴方程ax2+bx+c=0有一根为-3,故④正确.
综上所述,正确的是①②④.
故答案为:①②④.
点评:本题考查了二次函数的性质,主要利用了二次函数与x轴的交点问题,利用二次函数图象求解一元二次不等式,利用特殊值法确定函数值,综合题,但难度不大.

练习册系列答案
相关题目
若(1-2a)2+
=0,则ab的值为( )
| b+2 |
| A、-2 | ||
B、
| ||
| C、-1 | ||
| D、1 |
下列数字中是中心对称的是( )
A、 |
B、 |
C、 |
D、 |
如果点P(-5,y)在第三象限,则y的取值范围是( )
| A、y>0 | B、y<0 |
| C、y≤0 | D、y≥0 |
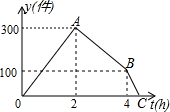 某种产品从生产流水线上下线后,需要包装人库,通常的办法是,流水线先工作一段时间,包装工人再开始工作.某次包装工人工作一段时间后,因临近下班,又抽调了一部分工人来帮忙,使包装人库的速度提高了一倍.如图是下线后待包装人库的产品数量y(件)与流水线开始工作时间t(h)的函数关系的图象.以下结论正确的有
某种产品从生产流水线上下线后,需要包装人库,通常的办法是,流水线先工作一段时间,包装工人再开始工作.某次包装工人工作一段时间后,因临近下班,又抽调了一部分工人来帮忙,使包装人库的速度提高了一倍.如图是下线后待包装人库的产品数量y(件)与流水线开始工作时间t(h)的函数关系的图象.以下结论正确的有