题目内容
【题目】我们已经知道(a﹣b)2≥0,即a2﹣2ab+b2≥0.所以a2+b2≥2ab(当且仅当a=b时取等号).
阅读1:若a、b为实数,且a>0,b>0.
∵(![]() )2≥0,∴a﹣2
)2≥0,∴a﹣2![]() +b≥0,∴a+b≥2
+b≥0,∴a+b≥2![]() (当且仅当a=b时取等号).
(当且仅当a=b时取等号).
阅读2:若函数y=x![]() (m>0,x>0,m为常数).由阅读1结论可知:x
(m>0,x>0,m为常数).由阅读1结论可知:x![]() 即x
即x![]() ∴当x
∴当x![]() 即x2=m,∴x=
即x2=m,∴x=![]() (m>0)时,函数y=x
(m>0)时,函数y=x![]() 的最小值为2
的最小值为2![]() .
.
阅读理解上述内容,解答下列问题:
问题1:当x>0时,![]() 的最小值为 ;当x<0时,
的最小值为 ;当x<0时,![]() 的最大值为 .
的最大值为 .
问题2:函数y=a+![]() (a>1)的最小值为 .
(a>1)的最小值为 .
问题3:求代数式![]() (m>﹣2)的最小值,并求出此时的m的值.
(m>﹣2)的最小值,并求出此时的m的值.
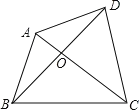
问题4:如图,四边形ABCD的对角线AC,BD相交于点O,△AOB、△COD的面积分别为4和16,求四边形ABCD面积的最小值.
【答案】(1)2,-2;(2)9;(3)最小值是4,m=0;(4)36.
【解析】
(1)当x>0时,按照公式a+b≥2![]() (当且仅当a=b时取等号)来计算即可;x<0时,由于x>0,
(当且仅当a=b时取等号)来计算即可;x<0时,由于x>0,![]() >0,则也可以按照公式a+b≥2
>0,则也可以按照公式a+b≥2![]() (当且仅当a=b时取等号)来计算;
(当且仅当a=b时取等号)来计算;
(2)将y=a+![]() 变形为y=a-1+
变形为y=a-1+![]() +1,故可根据公式a+b≥2
+1,故可根据公式a+b≥2![]() (当且仅当a=b时取等号)进行求解;
(当且仅当a=b时取等号)进行求解;
(3)将代数式![]() 变形得
变形得![]() ,故可根据公式a+b≥2
,故可根据公式a+b≥2![]() (当且仅当a=b时取等号)进行求解;
(当且仅当a=b时取等号)进行求解;
(4)设S△BOC=x,已知S△AOB=4,S△COD=16,则由等高三角形可知:S△BOC:S△COD=S△AOB:S△AOD,用含x的式子表示出S△AOD,四边形ABCD的面积用含x的代数式表示出来,再按照题中所给公式求得最小值,加上常数即可.
(1)当x>0时,![]() ≥2
≥2![]() =2;
=2;
当x<0时,![]() =(x
=(x![]() )
)
∵x![]() ≥2
≥2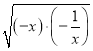 =2
=2
∴(x![]() )≤2
)≤2
∴当x>0时,x+![]() 的最小值为2;当x<0时,x+
的最小值为2;当x<0时,x+![]() 的最大值为2.
的最大值为2.
故答案为:2;2;
(2)y=a+![]() = a-1+
= a-1+![]() +1
+1
∵a-1>0
∴y=a-1+![]() +1≥
+1≥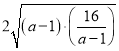 +1=2×4+1=9
+1=2×4+1=9
故答案为:9;
(3)![]() =
=![]()
∵m>﹣2,
∴![]() ≥
≥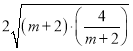 =4
=4
当m+2=![]() 时成立,即m=0(-4舍去)时,最小值为4.
时成立,即m=0(-4舍去)时,最小值为4.
(4)设S△BOC=x,已知S△AOB=4,S△COD=16
则由等高三角形可知:S△BOC:S△COD=S△AOB:S△AOD
∴x:16=4:S△AOD
∴S△AOD=![]()
∴四边形ABCD面积=4+16+x+![]() ≥20+
≥20+![]() =36
=36
当且仅当x=8时取等号,即四边形ABCD面积的最小值为36.

 阅读快车系列答案
阅读快车系列答案