Question

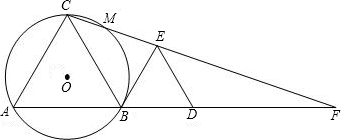
如图，已知AB是⊙O的直径，点E在⊙O上，过点E的直线EF与AB的延长线交于点F，AC⊥EF，垂足为C，AE平分∠FAC．
（1）求证：CF是⊙O的切线；
（2）∠F=30°时，求

S△OFE

S四边形AOEC

的值．

Answer 1

（1）证明：连接OE，
∵AE平分∠FAC，
∴∠CAE=∠OAE，
又∵OA=OE，∠OEA=∠OAE，∠CAE=∠OEA，
∴OE∥AC，
∴∠OEF=∠ACF，
又∵AC⊥EF，
∴∠OEF=∠ACF=90°，
∴OE⊥CF，
又∵点E在⊙O上，
∴CF是⊙O的切线；

（2）∵∠OEF=90°，∠F=30°，
∴OF=2OE
又OA=OE，
∴AF=3OE，
又∵OE∥AC，
∴△OFE∽△AFC，
∴

OE

AC

=

OF

AF

=

2

3

，
∴

S△OFE

S△AFC

=

4

9

，
∴

S△OFE

S四边形AOEC

=

4

5

．