题目内容
如图,平面直角坐标系中,点A、B、C在x轴上,点D、E在y轴上,OA=OD=2,OC=OE=4,DB⊥DC,直线AD与经过B、E、C三点的抛物线交于F、G两点,与其对称轴交于M.点P为线段FG上一个动点(与F、G不重合),PQ∥y轴与抛物线交于点Q.
(1)求经过B、E、C三点的抛物线的解析式;
(2)是否存在点P,使得以P、Q、M为顶点的三角形与△AOD相似?若存在,求出满足条件的点P的坐标;若不存在,请说明理由;
(3)若抛物线的顶点为N,连接QN,探究四边形PMNQ的形状:①能否成为菱形;②能否成为等腰梯形?若能,请直接写出点P的坐标;若不能,请说明理由.


【考点】二次函数综合题.
【专题】压轴题.
【分析】(1)在Rt△ODC中,根据射影定理即可求出OB的长,由此可得到B点的坐标,进而可用待定系数法求出抛物线的解析式;
(2)易知△AOD是等腰Rt△,若以P、Q、M为顶点的三角形与△AOD相似,那么△PQM也必须是等腰Rt△;由于∠QPM≠90°,因此本题分两种情况:
①PQ为斜边,M为直角顶点;②PM为斜边,Q为直角顶点;
首先求出直线AD的解析式,进而可得到M点的坐标;设出P点横坐标,然后根据抛物线和直线AD的解析式表示出P、Q的纵坐标,即可得到PQ的长;在①中,PQ的长为M、P横坐标差的绝对值的2倍;在②中,PQ的长正好等于M、P横坐标差的绝对值,由此可求出符合条件的P点坐标;
(3)①若四边形PQNM是菱形,首先必须满足四边形PMNQ是平行四边形,此时MN与PQ相等,由此可得到P点坐标,然后再判断PQ是否与PM相等即可;
②由于当NQ∥PM时,四边形PMNQ是平行四边形,因此本题只需考虑MN∥PQ这一种情况;若四边形PMNQ是等腰梯形且MN、PQ为上下底,那么根据等腰梯形的对称性可知:Q、P的纵坐标的和应该等于N、M的纵坐标的和,据此可求出P、Q的坐标,然后再判断QN与PM是否平行即可.
【解答】解:(1)在Rt△BDC中,OD⊥BC,
由射影定理,得:OD2=OB•OC;
则OB=
 =1;
=1;
∴B(﹣1,0);
∴B(﹣1,0),C(4,0),E(0,4);
设抛物线的解析式为:y=a(x+1)(x﹣4)(a≠0),则有:
a(0+1)(0﹣4)=4,a=﹣1;
∴y=﹣(x+1)(x﹣4)=﹣x2+3x+4;
(2)因为A(﹣2,0),D(0,2);
所以直线AD:y=x+2;
联立
 ,
,
解得
 或
或
 ,
,
则F(1﹣
 ,3﹣
,3﹣
 ),G(1+
),G(1+
 ,3+
,3+
 );
);
设P点坐标为(x,x+2)(1﹣
 <x<1+
<x<1+
 ),则Q(x,﹣x2+3x+4);
),则Q(x,﹣x2+3x+4);
∴PQ=﹣x2+3x+4﹣x﹣2=﹣x2+2x+2;
易知M(
 ,
,
 ),
),
若以P、Q、M为顶点的三角形与△AOD相似,则△PQM为等腰直角三角形;
①以M为直角顶点,PQ为斜边;PQ=2|xM﹣xP|,即:
﹣x2+2x+2=2(
 ﹣x),
﹣x),
解得x=2﹣
 ,x=2+
,x=2+
 (不合题意舍去)
(不合题意舍去)
∴P(2﹣
 ,4﹣
,4﹣
 );
);
②以Q为直角顶点,PM为斜边;PQ=|xM﹣xQ|,
即:﹣x2+2x+2=
 ﹣x,
﹣x,
解得x=
 ,x=
,x=
 (不合题意舍去)
(不合题意舍去)
∴P(
 ,
,
 )
)
故存在符合条件的P点,且P点坐标为(2﹣
 ,4﹣
,4﹣
 )或(
)或(
 ,
,
 );
);
(3)易知N(
 ,
,
 ),M(
),M(
 ,
,
 );
);
设P点坐标为(m,m+2),
则Q(m,﹣m2+3m+4);(1﹣
 <m<1+
<m<1+
 )
)
∴PQ=﹣m2+2m+2,NM=
 ;
;
①若四边形PMNQ是菱形,则首先四边形PMNQ是平行四边形,有:
MN=PQ,
即:﹣m2+2m+2=
 ,
,
解得m=
 ,m=
,m=
 (舍去);
(舍去);
当m=
 时,P(
时,P(
 ,
,
 ),Q(
),Q(
 ,
,
 )
)
此时PM=
 ≠MN,故四边形PMNQ不可能是菱形;
≠MN,故四边形PMNQ不可能是菱形;
②由于当NQ∥PM时,四边形PMNQ是平行四边形,
所以若四边形PMNQ是等腰梯形,只有一种情况:PQ∥MN;
依题意,则有:
 (yN﹣yQ)=
(yN﹣yQ)=
 (yP﹣yM),
(yP﹣yM),
即
 (yN+yM)=
(yN+yM)=
 (yP+yQ),
(yP+yQ),
即
 +
+
 =﹣m2+3m+4+m+2,
=﹣m2+3m+4+m+2,
解得m=
 ,m=
,m=
 (舍去);
(舍去);
当m=
 时,P(
时,P(
 ,
,
 ),Q(
),Q(
 ,
,
 ),此时NQ与MP不相等,
),此时NQ与MP不相等,
∴四边形PMNQ可以是等腰梯形,且P点坐标为(
 ,
,
 ).
).




【点评】此题是二次函数的综合题,考查的知识点有:直角三角形的性质,二次函数的确定,等腰三角形、菱形、等腰梯形的判定和性质等,同时还考查了分类讨论的数学思想;要特别注意的是在判定梯形的过程中,不要遗漏证明另一组对边不平行的条件.

 的长为2π,则∠ACB的大小是 .
的长为2π,则∠ACB的大小是 .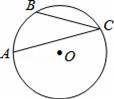





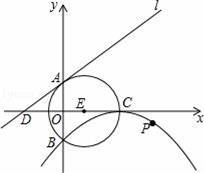
 ,1) B.(1,﹣
,1) B.(1,﹣



 ÷(2﹣
÷(2﹣
 ),其中x=
),其中x=
 +1.
+1.
 ,则
,则
 =
= 


 的解集是( )
的解集是( )