Question

【题目】如图1，在矩形中，，，动点从出发，以每秒1个单位的速度沿射线方向移动，作关于直线的对称，设点的运动时间为．

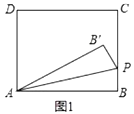
（1）当时．

①如图2．当点落在上时，显然是直角三角形，求此时的值；

②当点不落在上时，请直接写出是直角三角形时的值；

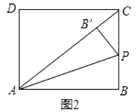
（2）若直线与直线相交于点，且当时，．问：当时，的大小是否发生变化，若不变，请说明理由．

Answer 1

【答案】（1）①，②或或；（2）不变，见解析

【解析】

（1）①利用勾股定理求出AC，再根据折叠的性质以及勾股定理即可得出答案；②分三种情况进行讨论：①如图2-1中，当时，②如图2-2中，当时，③如图2-3中，当时，在中分别找出每条边的长度，再利用勾股定理建立方程求解即可得出答案；

（2）首先证明ABCD是正方形，再利用全等三角形的性质以及折叠的性质即可得出答案．

解：（1）①如图1中，∵四边形是矩形，

∴，∴

∵翻折

∴，，

∴，

∴在中，

∴

∴；

②如图2-1中，当，在上时，

∵四边形是矩形，∴，，，

∴

∴

在中，∵，

∴，

∴．

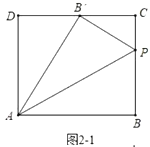
如图2-2中，当，在的延长线上时，

在中，，

∴

在中，则有：，

解得．

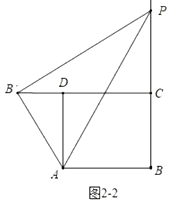
如图2-3中，当时，

易证四边形为正方形，则．

综上所述，满足条件的的值为或或；

（2）当时，如图，∵

∴，

∵翻折，

∴，，

又∵，

∴，

∴，即四边形是正方形，

当时，如图，设

∴，

∴，

易证，

∴，

∵翻折，

∴，

∴，

∴，

∴．