题目内容
如图1,梯形ABCD中,AD∥BC,∠ABC=90°,且AD=1,AB=BC=2,对角线AC和BD相交于点O.点E在AB上,点F在CB延长线上,连结EF,且BE=BF.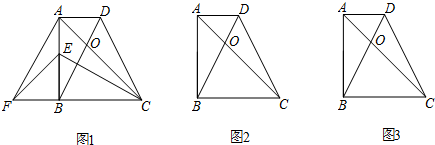
(1)连结AF,CE,则线段AF与CE的位置关系是
(2)将图1中的△EBF绕点B逆时针方向旋转旋转α角(0°<α<90°),连结AF、CE.试在图2中画出旋转后的图形,并判断此时(1)中的两个结论是否成立,写出你的猜想并加以证明;
(3)将图1中的△EBF绕点B逆时针旋转,使到一边BF落在线段BO上,此时△EBF的一边EF与BC交于点M,连结AF、CE.试在图3中画出旋转后的图形,并解答下列问题:
①此时(1)中的两个结论是否成立?(直接写出你的猜想,不必证明.)
②已知OF=
| ||
| 6 |
分析:(1)延长CE交AF于M,证△ABF≌△CBE,推出AF=CE,∠CEB=∠AFB,求出∠ECB+∠AFB=90°,根据三角形内角和定理求出∠CMF=90°即可;
(2)(1)中的两个结论仍然成立,求出∠CBE=∠ABF,证△ABF≌△CBE.推出AF=CE,∠1=∠2,求出∠AMC=90°即可;
(3)①两个结论仍然成立;②在Rt△DAB中,求出BD=
,证△AOD∽△COB,求出
=
,求出OB=
BD=
,BE=
,证△BME∽△BOA,得出
=
,即可求出BM.
(2)(1)中的两个结论仍然成立,求出∠CBE=∠ABF,证△ABF≌△CBE.推出AF=CE,∠1=∠2,求出∠AMC=90°即可;
(3)①两个结论仍然成立;②在Rt△DAB中,求出BD=
| 5 |
| OD |
| OB |
| 1 |
| 2 |
| 2 |
| 3 |
| 2 |
| 3 |
| 5 |
| ||
| 2 |
| BM |
| OB |
| BE |
| BA |
解答:解:(1)AF⊥CE,AF=CE,
理由是:延长CE交AF于M,
∵∠ABC=90°,
∴∠ABF=90°,
在△ABF和△CBE中
∴△ABF≌△CBE(SAS),
∴AF=CE,∠CEB=∠AFB,
∵∠EBC=90°,
∴∠ECB+∠CEB=90°,
∴∠ECB+∠AFB=90°,
∴∠CMF=180°-90°=90°,
∴AF⊥CE;,
故答案为:垂直,相等;
(2)猜想:(1)中的两个结论仍然成立.
证明:∵∠ABC=∠EBF=90°,
∴∠ABC+∠ABE=∠EBF+∠ABE,
∴∠CBE=∠ABF,
在△ABF和△CBE中,
∴△ABF≌△CBE(SAS).
∴AF=CE,∠1=∠2,
∵∠1+∠3=90°,∠3=∠4,
∴∠3+∠4=90°,
∴∠AMC=90°,
∴AF⊥CE;
(3)①(1)中的两个结论仍然成立;
②在Rt△DAB中,BD=
=
=
,
∵AD∥BC,
∴△AOD∽△COB.
∴
=
,
∵AD=1,BC=2,
∴
=
,
∴OB=
BD=
,
∵OF=
,
∴BE=BF=OB-OF=
,
∵∠1+∠FBM=90°,∠2+∠FBM=90°,
∴∠1=∠2,
又∵∠3=∠BAO=45°,
∴△BME∽△BOA,
∴
=
,
∴
=
∴BM=
.
理由是:延长CE交AF于M,
∵∠ABC=90°,
∴∠ABF=90°,
在△ABF和△CBE中
|
∴△ABF≌△CBE(SAS),
∴AF=CE,∠CEB=∠AFB,
∵∠EBC=90°,
∴∠ECB+∠CEB=90°,
∴∠ECB+∠AFB=90°,
∴∠CMF=180°-90°=90°,
∴AF⊥CE;,
故答案为:垂直,相等;
(2)猜想:(1)中的两个结论仍然成立.
证明:∵∠ABC=∠EBF=90°,
∴∠ABC+∠ABE=∠EBF+∠ABE,
∴∠CBE=∠ABF,
在△ABF和△CBE中,
|
∴△ABF≌△CBE(SAS).
∴AF=CE,∠1=∠2,
∵∠1+∠3=90°,∠3=∠4,
∴∠3+∠4=90°,
∴∠AMC=90°,
∴AF⊥CE;

(3)①(1)中的两个结论仍然成立;
②在Rt△DAB中,BD=
| AB2+AD2 |
| 1+4 |
| 5 |
∵AD∥BC,
∴△AOD∽△COB.
∴
| AD |
| BC |
| OD |
| OB |
∵AD=1,BC=2,
∴
| OD |
| OB |
| 1 |
| 2 |
∴OB=
| 2 |
| 3 |
| 2 |
| 3 |
| 5 |
∵OF=
| ||
| 6 |
∴BE=BF=OB-OF=
| ||
| 2 |
∵∠1+∠FBM=90°,∠2+∠FBM=90°,
∴∠1=∠2,
又∵∠3=∠BAO=45°,
∴△BME∽△BOA,
∴
| BM |
| OB |
| BE |
| BA |
∴
| BM | ||||
|
| ||||
| 2 |
∴BM=
| 5 |
| 6 |
点评:本题考查了勾股定理,相似三角形的性质和判定,全等三角形的性质和判定,三角形内角和定理,等腰直角三角形的应用,主要考查学生综合运用定理进行推理的 能力,题目比较典型,证明过程类似.

练习册系列答案
相关题目
 如图,在梯形ABCD中,AD∥BC,AB=DC=AD,AC=BC,求∠ACB的度数.
如图,在梯形ABCD中,AD∥BC,AB=DC=AD,AC=BC,求∠ACB的度数. 如图,在梯形ABCD中,AD∥BC,BC=30cm,动点M从A点开始沿AD边向D以1cm/s的速度运动,动点N从C点开始沿CB边向B以3cm/s的速度运动,M、N分别从A、C同时出发,当其中一点到端点时,另一点也随之停止运动,设运动时间为t s,t为何值时,四边形ABNM是平行四边形?
如图,在梯形ABCD中,AD∥BC,BC=30cm,动点M从A点开始沿AD边向D以1cm/s的速度运动,动点N从C点开始沿CB边向B以3cm/s的速度运动,M、N分别从A、C同时出发,当其中一点到端点时,另一点也随之停止运动,设运动时间为t s,t为何值时,四边形ABNM是平行四边形? 如图,在梯形ABCD中,AD∥BC,AB=DC,∠ACB=40°,∠ACD=30°,则∠B=
如图,在梯形ABCD中,AD∥BC,AB=DC,∠ACB=40°,∠ACD=30°,则∠B=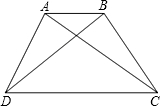 如图,在梯形ABCD中,AB∥CD,AD=BC,AC⊥BD,AB+CD=20,求梯形ABCD的面积.
如图,在梯形ABCD中,AB∥CD,AD=BC,AC⊥BD,AB+CD=20,求梯形ABCD的面积. 如图,等腰梯形ABCD中,AD=2,BC=6,高DF=2,则腰长DC=
如图,等腰梯形ABCD中,AD=2,BC=6,高DF=2,则腰长DC=