题目内容
已知:如图,在半径为![]() 的⊙O内
的⊙O内![]() ,有互相垂直的两条弦AB,CD,它们相交于P点.
,有互相垂直的两条弦AB,CD,它们相交于P点.
(1)求证:PA·PB=PC·PD;
(2)设BC的中点为F,连接FP并延长交AD于E,求证:EF![]() AD;
AD;
(3)如果AB=8,CD=6,求O、P两点之间的距离.

.
(1)证明:
∵∠A,∠C所对的圆弧相同,
 ∴∠A =∠C .
∴∠A =∠C .
∵AB![]() CD,
CD,
∴Rt△APD∽Rt△CPB .
∴![]() .
.
∴PA·PB=PC·PD.
(2)证明:
![]() ∵F为BC的中点,△CPB为直角三角形,
∵F为BC的中点,△CPB为直角三角形,
∴PF=FC,∠CPF =∠C .
又∵∠A =∠C,∠DPE =∠CPF,
∴∠A =∠DPE .
∵∠A +∠D=90°,
∴∠DPE +∠D=90°.
∴EF![]() AD .
AD .
(3)解:作OM![]() AB于M, ON
AB于M, ON![]() CD于N,
CD于N,
∴OMPN为矩形.
连接OB,OD,OP,由垂径定理,得AM=BM=4,CN=DN=3.
由勾股定理,得![]() ,
,![]() .
.
∴![]() .
.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 于点E,且EM>MC.连接DE,DE=
于点E,且EM>MC.连接DE,DE=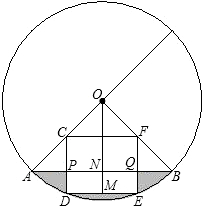 已知:如图,在半径为4的⊙O中,圆心角∠AOB=90°,以半径OA、OB的中点C、F为顶点作矩形CDEF,顶点D、E在⊙O的劣弧
已知:如图,在半径为4的⊙O中,圆心角∠AOB=90°,以半径OA、OB的中点C、F为顶点作矩形CDEF,顶点D、E在⊙O的劣弧
 上滑动并保持AE=CF,但点F不与A、C重合,点E不与A、B重合.
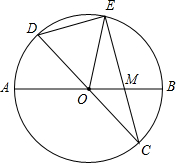
上滑动并保持AE=CF,但点F不与A、C重合,点E不与A、B重合.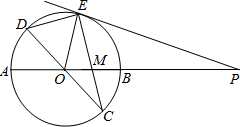 已知:如图,在半径为4的⊙O中,AB,CD是两条直径,M为OB的中点,CM的延长线交⊙O于点E,且EM>MC.连接DE,DE=
已知:如图,在半径为4的⊙O中,AB,CD是两条直径,M为OB的中点,CM的延长线交⊙O于点E,且EM>MC.连接DE,DE=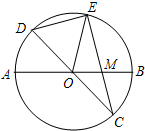 已知:如图,在半径为8的⊙O中,AB,CD是两条直径,M为OB的中点,CM的延长线交⊙O于点E,且EM>MC.连接DE,DE=
已知:如图,在半径为8的⊙O中,AB,CD是两条直径,M为OB的中点,CM的延长线交⊙O于点E,且EM>MC.连接DE,DE=