题目内容
如图:将△ABC纸片沿DE折叠成图①,此时点A落在四边形BCDE内部,则∠A与∠1、∠2之间有一种数量关系保持不变,
1.请找出这种数量关系并说明理由.
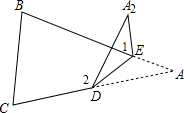
2.若折成图②或图③,即点A落在BE或CD上时,分别写出∠A与∠2;∠A与∠1之间的关系;(不必证明)
3.若折成图④,写出∠A与∠1、∠2之间的关系式;(不必证明);若折成图⑤,写出∠A与∠1、∠2之间的关系式.(不必证明)





1.∠1+∠2=2∠A
2.∠2=2∠A ,∠1=2∠A
3.∠2-∠1=2∠A ∠1-∠2=2∠A
解析:
(1)解:延长BD、CE,交于点P;
则△BCP即为折叠前的三角形,
由折叠的性质知:∠DAE=∠DPE.
图①中:连接AP;
由三角形的外角性质知:
∠1=∠DAP+∠DPA,∠2=∠EAP+∠EPA;
则∠1+∠2=∠DAE+∠DPE=2∠DAE,
即∠1+∠2=2∠A. (4分,酌情给分)
(2)∠2=2∠A ,∠1=2∠A (2分)
(3)∠2-∠1=2∠A ∠1-∠2=2∠A (2分)

练习册系列答案
相关题目
 如图,将△ABC纸片沿着线段DE折叠,使点A落在点A′处,若∠A′DE=∠C,A′D=4,A′E=3,DB=6,BC=12,求折痕DE的长.
如图,将△ABC纸片沿着线段DE折叠,使点A落在点A′处,若∠A′DE=∠C,A′D=4,A′E=3,DB=6,BC=12,求折痕DE的长.
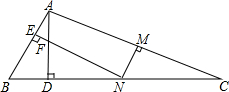 (2010•太原二模)如图,将△ABC纸片沿MN折叠后点C与点A恰好重合,设∠C=22.5°,AD⊥BC于点D.过点N作NE⊥AB于点E,并且交AD于点F,求证:DB=DF.
(2010•太原二模)如图,将△ABC纸片沿MN折叠后点C与点A恰好重合,设∠C=22.5°,AD⊥BC于点D.过点N作NE⊥AB于点E,并且交AD于点F,求证:DB=DF.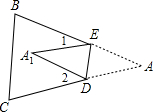
 如图,将△ABC纸片沿DE折叠后,点A落在BC边上的A′处,若点D为AB边的中点,BC=5,则DE等于( )
如图,将△ABC纸片沿DE折叠后,点A落在BC边上的A′处,若点D为AB边的中点,BC=5,则DE等于( )