题目内容
如图，将△ABC纸片沿着线段DE折叠，使点A落在点A′处，若∠A′DE=∠C，A′D=4，A′E=3，DB=6，BC=12，求折痕DE的长．
分析：根据折叠的性质，得△ADE≌△A′DE，则∠ADE=∠A′DE，AD=A′D，AE=A′E；再根据相似三角形的判定及性质进行求解．
解答：解：根据题意，得
△ADE≌△A′DE．
∴∠ADE=∠A′DE，AD=A′D=4，AE=A′E=3．
又∠A′DE=∠C，
∴∠ADE=∠C．
又∠A=∠A，
∴△ADE∽△ACB．
=
=
，
即
=
，
DE=3.6．
△ADE≌△A′DE．
∴∠ADE=∠A′DE，AD=A′D=4，AE=A′E=3．
又∠A′DE=∠C，
∴∠ADE=∠C．
又∠A=∠A，
∴△ADE∽△ACB．
| DE |
| BC |
| AE |
| AB |
| AD |
| AC |
即
| DE |
| 12 |
| 3 |
| 10 |
DE=3.6．
点评：此题综合运用了折叠的性质、相似三角形的判定以及性质．
练习册系列答案
名校课堂系列答案
相关题目
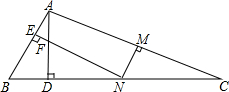（2010•太原二模）如图，将△ABC纸片沿MN折叠后点C与点A恰好重合，设∠C=22.5°，AD⊥BC于点D．过点N作NE⊥AB于点E，并且交AD于点F，求证：DB=DF．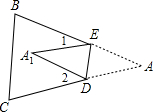
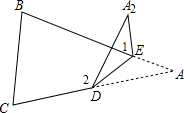
如图，将△ABC纸片沿DE折叠后，点A落在BC边上的A′处，若点D为AB边的中点，BC=5，则DE等于（ ）