题目内容
如图1,在△ABC中,∠ACB=90°,BC=AC,若MN是经过点C的直线,AD⊥MN于D,BE⊥MN于E.
(1)求证:DE=AD+BE.
(2)若将MN绕C旋转,使MN与AB相交,其他条件都不变,AD与CE边相等吗?(见图2).
(3)在图2中,证明AD、BE和DE有何关系?直接写出答案.

(1)求证:DE=AD+BE.
(2)若将MN绕C旋转,使MN与AB相交,其他条件都不变,AD与CE边相等吗?(见图2).
(3)在图2中,证明AD、BE和DE有何关系?直接写出答案.

考点:全等三角形的判定与性质,等腰直角三角形
专题:几何综合题
分析:(1)求出∠ACB=∠ADC=∠BEC=90°,∠DAC=∠ECB,根据AAS推出即可;
(2)根据全等三角形的性质得出即可;
(3)根据全等三角形性质得出AD=CE,BE=CD,即可求出答案.
(2)根据全等三角形的性质得出即可;
(3)根据全等三角形性质得出AD=CE,BE=CD,即可求出答案.
解答:(1)证明:AD⊥MN,BE⊥MN,∠ACB=90°,
∴∠ACB=∠ADC=∠BEC=90°,
∴∠DAC+∠DCA=90°,∠ACD+∠ECB=90°,
∴∠DAC=∠ECB,
在△ADC和△CEB中,
∴△ADC≌△CEB(AAS),
∴DC=BE,AD=CE,
∴DE=DC+CE=AD+BE.
(2)解:AD=CE,
理由是:AD⊥MN,BE⊥MN,∠ACB=90°,
∴∠ACB=∠ADC=∠BEC=90°,
∴∠DAC+∠DCA=90°,∠ACD+∠ECB=90°,
∴∠DAC=∠ECB,
在△ADC和△CEB中
∴△ADC≌△CEB(AAS),
∴AD=CE;
(3)DE=AD-BE,
证明:∵△ADC≌△CEB,
∴AD=CE,BE=CD,
∵DE=CE-CD,
∴DE=AD-BE.
∴∠ACB=∠ADC=∠BEC=90°,
∴∠DAC+∠DCA=90°,∠ACD+∠ECB=90°,
∴∠DAC=∠ECB,
在△ADC和△CEB中,
|
∴△ADC≌△CEB(AAS),
∴DC=BE,AD=CE,
∴DE=DC+CE=AD+BE.

(2)解:AD=CE,
理由是:AD⊥MN,BE⊥MN,∠ACB=90°,
∴∠ACB=∠ADC=∠BEC=90°,
∴∠DAC+∠DCA=90°,∠ACD+∠ECB=90°,
∴∠DAC=∠ECB,
在△ADC和△CEB中
|
∴△ADC≌△CEB(AAS),
∴AD=CE;
(3)DE=AD-BE,
证明:∵△ADC≌△CEB,
∴AD=CE,BE=CD,
∵DE=CE-CD,
∴DE=AD-BE.
点评:本题考查了全等三角形的性质和判定的应用,注意:全等三角形的判定定理有SAS,ASA,SSS,AAS,全等三角形的对应边相等.

练习册系列答案
相关题目
下列性质矩形不一定具备的是( )
| A、对角线相等 |
| B、四个内角都相等 |
| C、对角线互相平分 |
| D、对角线互相垂直 |
有一个样本有100个数据,落在某一组内的频率是0.3,那么落在这一组内的频数是( )
| A、50 | B、30 | C、15 | D、3 |
 平行四边形ABCD中,AB∥CD,GM、GN、HM、HN分别平分∠AGH、∠BGH、∠CHG、∠DHG,试判断四边形GMHN的形状,并说明你的理由.
平行四边形ABCD中,AB∥CD,GM、GN、HM、HN分别平分∠AGH、∠BGH、∠CHG、∠DHG,试判断四边形GMHN的形状,并说明你的理由. 如图,△ABC中,AD平分∠BAC,∠1=∠2,求证:AB=AC.
如图,△ABC中,AD平分∠BAC,∠1=∠2,求证:AB=AC.
 数学课上,神奇而有魔力的黄金分割点激起了同学们极大的兴趣,某学习兴趣小组在探究该知识时,由黄金分割点联想到黄金分割线,类似的给出定义:直线AB将一个面积为S的图形分成两部分,这两部分的面积分别为S1和S2,如果S1:S2=S1:S(S1>S2),那么称直线AB为该图的黄金分割线.
数学课上,神奇而有魔力的黄金分割点激起了同学们极大的兴趣,某学习兴趣小组在探究该知识时,由黄金分割点联想到黄金分割线,类似的给出定义:直线AB将一个面积为S的图形分成两部分,这两部分的面积分别为S1和S2,如果S1:S2=S1:S(S1>S2),那么称直线AB为该图的黄金分割线.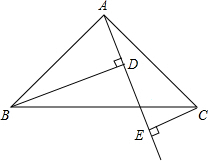 如图,在Rt△ABC中,∠BAC=90°,AB=AC,AE是过A点的一条直线,且B点和C点在AE的两侧,BD⊥AE于点D,CE⊥AE于点E,CE=2,BD=6,求DE的长.
如图,在Rt△ABC中,∠BAC=90°,AB=AC,AE是过A点的一条直线,且B点和C点在AE的两侧,BD⊥AE于点D,CE⊥AE于点E,CE=2,BD=6,求DE的长.