题目内容
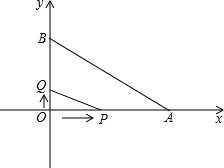 如图,在平面直角坐标系中,点A(4,0)、B(0,3),动点P、Q同时从原点O出发,其中点P沿线段OA向终点A运动,速度为
如图,在平面直角坐标系中,点A(4,0)、B(0,3),动点P、Q同时从原点O出发,其中点P沿线段OA向终点A运动,速度为| 3 |
考点:圆的综合题,解一元一次不等式组,勾股定理,直线与圆的位置关系,平行线分线段成比例,锐角三角函数的定义
专题:
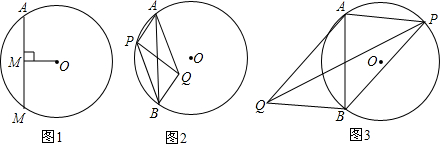
分析:以PQ为直径作⊙M,过点M作MH⊥AB于H,过点Q作QD⊥AB于D,过点P作PC⊥AB于C,易得QD∥MH∥PC,MQ=MP.根据平行线分线段成比例得CH=DH,再根据梯形的中位线定理可得MH=
(QD+PC).然后利用三角函数将DQ、PC用t的代数式表示,进而用t的代数式表示出MH,由⊙M与线段AB有两个公共点可得MH<
PQ,从而得到t的一个范围,再由其中一个点到终点时另一个点也随之停止可得t的又一个取值范围,就可解决问题.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:以PQ为直径作⊙M,过点M作MH⊥AB于H,
过点Q作QD⊥AB于D,过点P作PC⊥AB于C,如图所示.
则有QD∥MH∥PC,MQ=MP.
根据平行线分线段成比例得:CH=DH.
由梯形中位线定理可得:MH=
(QD+PC).
由题可得:OA=4,OB=3,OP=
t,OQ=t.
则有BQ=3-t,AP=4-
t.
∵∠AOB=90°,∴AB=5,PQ=
=2t.
由sin∠OBA=
=
得:QD=
(3-t)=
.
由sin∠OAB=
=
得:PC=
(4-
t)=
.
∴MH=
(
+
)=
.
由⊙M与线段AB有两个公共点可得:MH<
PQ.
则有
<t.
解得:t>
.
由其中一个点到终点时另一个点也随之停止可得:
.
解得:t≤
.
∴t的取值范围是
<t≤
.
故答案为:
<t≤
.
过点Q作QD⊥AB于D,过点P作PC⊥AB于C,如图所示.

则有QD∥MH∥PC,MQ=MP.
根据平行线分线段成比例得:CH=DH.
由梯形中位线定理可得:MH=
| 1 |
| 2 |
由题可得:OA=4,OB=3,OP=
| 3 |
则有BQ=3-t,AP=4-
| 3 |
∵∠AOB=90°,∴AB=5,PQ=
| t2+3t2 |
由sin∠OBA=
| OA |
| AB |
| QD |
| BQ |
| 4 |
| 5 |
| 12-4t |
| 5 |
由sin∠OAB=
| PC |
| PA |
| OB |
| AB |
| 3 |
| 5 |
| 3 |
12-3
| ||
| 5 |
∴MH=
| 1 |
| 2 |
| 12-4t |
| 5 |
12-3
| ||
| 5 |
24-(4+3
| ||
| 10 |
由⊙M与线段AB有两个公共点可得:MH<
| 1 |
| 2 |
则有
24-(4+3
| ||
| 10 |
解得:t>
336-72
| ||
| 169 |
由其中一个点到终点时另一个点也随之停止可得:
|
解得:t≤
4
| ||
| 3 |
∴t的取值范围是
336-72
| ||
| 169 |
4
| ||
| 3 |
故答案为:
336-72
| ||
| 169 |
4
| ||
| 3 |
点评:本题考查了直线与圆的位置关系、平行线分线段成比例、锐角三角函数的定义、勾股定理、解不等式组等知识,而利用梯形中位线定理表示出圆心到直线的距离是解决本题的关键.

练习册系列答案
相关题目
 如图所示,AB、CD相交于点O.OB平分∠DOE,若∠DOE=63°12′,则∠AOC的度数是
如图所示,AB、CD相交于点O.OB平分∠DOE,若∠DOE=63°12′,则∠AOC的度数是 如图,AC⊥BC,垂足为C,AC=6cm,BC=8cm,AB=10cm,点A到BC所在直线的距离是
如图,AC⊥BC,垂足为C,AC=6cm,BC=8cm,AB=10cm,点A到BC所在直线的距离是 如图,阴影部分是以直角三角形的三边为直径的半圆,面积和为100,则最大的半圆面积是
如图,阴影部分是以直角三角形的三边为直径的半圆,面积和为100,则最大的半圆面积是