题目内容
 (2012•武侯区一模)如图,直线y=2x与双曲线y=
(2012•武侯区一模)如图,直线y=2x与双曲线y=| k |
| x |
| k |
| x |
(1)求直线BC的解析式;
(2)若
| AO |
| BC |
分析:(1)根据直线平移的规律,即可得出直线BC的解析式;
(2)根据反比例函数的性质得出A,B两点的坐标,根据xy=k即可得出k的值.
(2)根据反比例函数的性质得出A,B两点的坐标,根据xy=k即可得出k的值.
解答:解:(1)∵将直线y=2x向右平移3个单位后,得到的直线是BC,
∴直线BC的解析式是:y=2(x-3);
(2)过点A作AD⊥x轴于点D,BE⊥x轴于点E,
∵直线BC是由直线OA平移得到的,
∴
=
,
∵
=2,
∴
=2,
∴AD=2BE,
又∵直线BC的解析式是:y=2(x-3),
∴设B点的横坐标为3+x,
∴B点的纵坐标为:y=2(x+3-3)=2x,
∴BE=2x,
∵AD=2BE,
∴AD=4x,
∵y=2x,
∴
=2,
∴OD=
AD=2x,
∴A点的纵坐标为:4x,
根据A,B都在反比例函数图象上得出:
∴2x×4x=(3+x)×2x,
x=1,
∴k的值为:2×1×4×1=8.
∴直线BC的解析式是:y=2(x-3);
(2)过点A作AD⊥x轴于点D,BE⊥x轴于点E,
∵直线BC是由直线OA平移得到的,
∴
| AD |
| BE |
| AO |
| BC |
∵
| AO |
| BC |
∴
| AD |
| BE |

∴AD=2BE,
又∵直线BC的解析式是:y=2(x-3),
∴设B点的横坐标为3+x,
∴B点的纵坐标为:y=2(x+3-3)=2x,
∴BE=2x,
∵AD=2BE,
∴AD=4x,
∵y=2x,
∴
| AD |
| OD |
∴OD=
| 1 |
| 2 |
∴A点的纵坐标为:4x,
根据A,B都在反比例函数图象上得出:
∴2x×4x=(3+x)×2x,
x=1,
∴k的值为:2×1×4×1=8.
点评:此题主要考查了反比例函数的性质,用x表示出A,B两点的坐标,进而利用反比例函数的性质xy=k是解决问题的关键.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
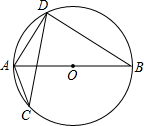 (2012•武侯区一模)如图,⊙O的弦CD与直径AB相交,若∠ACD=35°,则∠BAD=( )
(2012•武侯区一模)如图,⊙O的弦CD与直径AB相交,若∠ACD=35°,则∠BAD=( )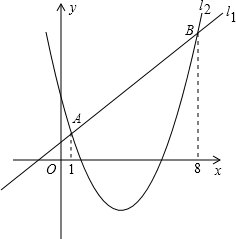 (2012•武侯区一模)如图,直线
(2012•武侯区一模)如图,直线