题目内容
19.“端午节”吃粽子是我国流传了上千年的习俗.某班学生在“端午节”前组织了一次综合实践活动,购买了一些材料制作爱心粽,每人从自己制作的粽子的个数,将制作粽子数量相同的学生分为一组,全班学生可分为A、B、C、D四个组,各组每人制作的粽子个数分别为4、5、6、7.根据下面不完整的统计图解答下列问题: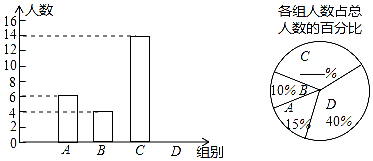
(1)请补全上面两统计图;
(2)该班学生制作粽子个数的平均数是6个;
(3)若全校2000名同学一起制作粽子,这次端午节全校同学共送给敬老院的老人12000个粽子.
分析 (1)根据统计图中的数据可以分别求得统计图中的未知数据,从而可以解答本题;
(2)根据统计图中的数据和加权平均数的计算方法可以解答本题;
(3)根据(2)中的平均数,可以求得全校2000名同学一起制作粽子,这次端午节全校同学共送给敬老院的老人的粽子数.
解答  解:(1)由题意可得,
解:(1)由题意可得,
学生总数为:6÷15%=40,
∴D组学生为:40-6-4-14=16(人),
∴C组学生占的百分比为:14÷40×100%=35%,
D组学生占的百分比为:16÷40×100%=40%,
补全的统计图,如图右所示;
(2)由题意可得,
该班学生制作粽子个数的平均数是:$\frac{4×6+5×4+6×14+7×16}{40}$=6个,
故答案为:6个;
(3)由题意可得,
全校2000名同学一起制作粽子,这次端午节全校同学共送给敬老院的老人6×2000=12000(个)粽子,
故答案为:12000.
点评 本题考查条形统计图、扇形统计图、加权平均数,解答本题的关键是明确它们各自的含义,利用数形结合的思想解答.

练习册系列答案
相关题目
9.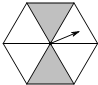 如图,一个正六边形转盘被分成六个全等的正三角形,任意转动这个转盘两次,指针均指向阴影区域的概率是( )
如图,一个正六边形转盘被分成六个全等的正三角形,任意转动这个转盘两次,指针均指向阴影区域的概率是( )
 如图,一个正六边形转盘被分成六个全等的正三角形,任意转动这个转盘两次,指针均指向阴影区域的概率是( )
如图,一个正六边形转盘被分成六个全等的正三角形,任意转动这个转盘两次,指针均指向阴影区域的概率是( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{9}$ | D. | $\frac{2}{9}$ |
7.下列各组整式中不是同类项的是( )
| A. | 3m2n与3nm2 | B. | $\frac{1}{3}$xy2与$\frac{1}{3}$x2y2 | C. | -5ab与-5×103ab | D. | 35与-12 |
11.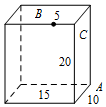 长方体的长为15,宽为10,高为20,点B在棱上与点C的距离为5,如图,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,则需要爬行的最短距离是( )
长方体的长为15,宽为10,高为20,点B在棱上与点C的距离为5,如图,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,则需要爬行的最短距离是( )
 长方体的长为15,宽为10,高为20,点B在棱上与点C的距离为5,如图,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,则需要爬行的最短距离是( )
长方体的长为15,宽为10,高为20,点B在棱上与点C的距离为5,如图,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,则需要爬行的最短距离是( )| A. | $10\sqrt{5}+5$ | B. | $5\sqrt{29}$ | C. | 25 | D. | $5\sqrt{37}$ |
9. 如图,小手盖住的点的坐标可以是( )
如图,小手盖住的点的坐标可以是( )
 如图,小手盖住的点的坐标可以是( )
如图,小手盖住的点的坐标可以是( )| A. | (5,2) | B. | (3,-4) | C. | (-4,-6) | D. | (-6,3) |
 如图,已知角α的终边上一点P的坐标为(a,2),且sinα=$\frac{2\sqrt{29}}{29}$,求α的值及角β的正弦值.
如图,已知角α的终边上一点P的坐标为(a,2),且sinα=$\frac{2\sqrt{29}}{29}$,求α的值及角β的正弦值.