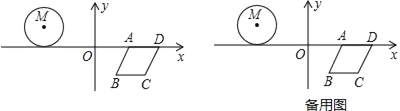
[题目]如图.在平面直角坐标系中.已知点A(2.1).B(﹣1.1).C(﹣1.﹣3).D(2.﹣3).点P从点A出发.以每秒1个单位长度的速度沿A﹣B﹣C﹣D﹣A-的规律在图边形ABCD的边上循环运动.则第2019秒时点P的坐标为( )A. (1.1)B. (0.1)C. (﹣1.1)D. (2.﹣1) 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】如图，在平面直角坐标系中，已知点A（2，1），B（﹣1，1），C（﹣1，﹣3），D（2，﹣3），点P从点A出发，以每秒1个单位长度的速度沿A﹣B﹣C﹣D﹣A…的规律在图边形ABCD的边上循环运动，则第2019秒时点P的坐标为（　　）

A. （1，1）B. （0，1）C. （﹣1，1）D. （2，﹣1）

【答案】C

【解析】

由点可得ABCD是长方形，点P从点A出发沿着A﹣B﹣C﹣D回到点A所走路程是14，即每过14秒点P回到A点一次，判断2019÷14的余数就是可知点P的位置．

解：由点A（2，1），B（﹣1，1），C（﹣1，﹣3），D（2，﹣3），

可知ABCD是长方形，

∴AB＝CD＝3，CB＝AD＝4，

∴点P从点A出发沿着A﹣B﹣C﹣D回到点A所走路程是：3+3+4+4＝14，

∵2019÷14＝144余3，

∴第2019秒时P点在B处，

∴P（﹣1，1）

故选：C．

练习册系列答案

（1）此次抽样调查中，共调查了多少名中学生家长；

（2）求出图2中扇形C所对的圆心角的度数，并将图1补充完整；

（3）根据抽样调查结果，请你估计我校11000名中学生家长中有多少名家长持反对态度；

（4）在此次调查活动中，初三（1）班和初三（2）班各有2位家长对中学生带手机持反对态度，现从中选2位家长参加学校组织的家校活动，用列表法或画树状图的方法求选出的2人来自不同班级的概率．

【题目】如图1，在直角三角形ABC中，∠ABC=90，将三角形ABC绕着点B逆时针旋转一定角度得到三角形BEF，EF交BC于点G．

（1）若，当∠ABE等于多少度时，；

（2）若，，，当时，

①求BG的长；

②连接AF交BE于点O，连接AE（如图2），设三角形EOF的面积为m，求三角形AEO的面积（用含m的代数式表示）

【题目】已知，如图，点C在线段AB上，且AC=6cm，BC=14cm，点M、N分别是AC、BC的中点．

（1）求线段MN的长度；

（2）在（1）中，如果AC=acm，BC=bcm，其它条件不变，你能猜测出MN的长度吗？请说出你发现的结论，并说明理由．

【题目】如图，已知数轴上点A表示的数为10， AB=16, 且B在A的左侧,动点P从点A出发，以每秒3个单位的速度沿数轴向左匀速运动，设运动时间为t(t>0）秒.

（1）写出数轴上点B表示的数_______

（2）线段AP的长为________（用含t的代数式表示）

（3）若动点Q从B出发，以每秒1个单位的速度沿数轴向右匀速运动，若P,Q同时出发，求运动多少秒时，P、Q相遇?

（4）若动点Q从B出发，以每秒1个单位的速度沿数轴向左匀速运动，若P,Q同时出发，求点P运动多少秒时追上点Q?

【题目】某区对2019年参加学业水平考试的3000名初中毕业生进行了一次视力抽样调查，绘制出如下频数分布表和频数分布直方图.某区2019年初中毕业生视力抽样频数分布表

视力	频数/人 50 50	频率 0.25 0.15
	60	0.30
		0.25
	10

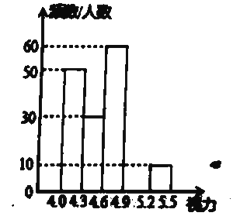
请根据图表信息回答下列问题：

（1）在频数分布表中，求的值和的值：

（2）将频数分布直方图补充完整；

（3）若视力在4.9以上（含4.9）均为正常，根据以上信息估计全区初中毕业生中

【题目】如图，⊙M与菱形ABCD在平面直角坐标系中，点M的坐标为（﹣3，1），点A的坐标为（2，0），点B的坐标为（1，﹣），点D在x轴上，且点D在点A的右侧．

（1）求菱形ABCD的周长；

（2）若⊙M沿x轴向右以每秒2个单位长度的速度平移，菱形ABCD沿x轴向左以每秒3个单位长度的速度平移，设菱形移动的时间为t（秒），当⊙M与AD相切，且切点为AD的中点时，连接AC，求t的值及∠MAC的度数；

（3）在（2）的条件下，当点M与AC所在的直线的距离为1时，求t的值．

【答案】（1）菱形的周长为8；（2）t=，∠MAC=105°；（3）当t=1﹣或t=1+时，圆M与AC相切．

【解析】试题分析：（1）过点B作BE⊥AD，垂足为E．由点A和点B的坐标可知：BE=，AE=1，依据勾股定理可求得AB的长，从而可求得菱形的周长；（2）记 M与x轴的切线为F，AD的中点为E．先求得EF的长，然后根据路程=时间×速度列出方程即可；平移的图形如图3所示：过点B作BE⊥AD，垂足为E，连接MF，F为 M与AD的切点．由特殊锐角三角函数值可求得∠EAB=60°，依据菱形的性质可得到∠FAC=60°，然后证明△AFM是等腰直角三角形，从而可得到∠MAF的度数，故此可求得∠MAC的度数；（3）如图4所示：连接AM，过点作MN⊥AC，垂足为N，作ME⊥AD，垂足为E．先求得∠MAE=30°，依据特殊锐角三角函数值可得到AE的长，然后依据3t+2t=5-AE可求得t的值；如图5所示：连接AM，过点作MN⊥AC，垂足为N，作ME⊥AD，垂足为E．依据菱形的性质和切线长定理可求得∠MAE=60°，然后依据特殊锐角三角函数值可得到EA=，最后依据3t+2t=5+AE．列方程求解即可．

试题解析：（）如图1所示：过点作，垂足为，

∵，，

∴，，

∴，

∵四边形为菱形，

∴，

∴菱形的周长．

（）如图2所示，⊙与轴的切线为，中点为，

∵，

∴，

∵，且为中点，

∴，，

∴，

解得．

平移的图形如图3所示：过点作，

垂足为，连接，为⊙与切点，

∵由（）可知，，，

∴，

∵四边形是菱形，

∴，

∵为切线，

∴，

∵为的中点，

∴，

∴是等腰直角三角形，

∴，

∴．

（）如图4所示：连接，过点作，垂足为，作，垂足为，

∵四边形为菱形，，

∴．

∵、是圆的切线

∴，

∵。

∴，

∴．

如图5所示：连接，过点作，垂足为，作，垂足为，

∵四边形为菱形，，

∴，

∵、是圆的切线，

∴，

∵，

∴，

∴．

综上所述，当或时，圆与相切．

点睛：此题是一道圆的综合题.圆中的方法规律总结：1、分类讨论思想：研究点、直线和圆的位置关系时，就要从不同的位置关系去考虑，即要全面揭示点、直线和元的各种可能的位置关系.这种位置关系的考虑与分析要用到分类讨论思想.1、转化思想：（1）化“曲面”为“平面”（2）化不规则图形面积为规则图形的面积求解.3、方程思想：再与圆有关的计算题中，除了直接运用公式进行计算外，有时根据图形的特点，列方程解答，思路清楚，过程简捷.

【题型】解答题
【结束】
28

【题目】如图1，在平面直角坐标系中，直线l与x轴、y轴分别交于点B（4，0）、C（0，3），点A为x轴负半轴上一点，AM⊥BC于点M交y轴于点N（0，）．已知抛物线y=ax2+bx+c经过点A，B，C．

（1）求抛物线的函数式；

（2）连接AC，点D在线段BC上方的抛物线上，连接DC，DB，若△BCD和△ABC面积满足S△BCD= S△ABC，求点D的坐标；

（3）如图2，E为OB中点，设F为线段BC上一点（不含端点），连接EF．一动点P从E出发，沿线段EF以每秒3个单位的速度运动到F，再沿着线段PC以每秒5个单位的速度运动到C后停止．若点P在整个运动过程中用时最少，请直接写出最少时间和此时点F的坐标．

【题目】如图是二次函数y=ax2+bx+c图象的一部分，其对称轴为x=﹣1，且过点（﹣3，0）．下列说法：①abc＜0；②2a﹣b=0；③4a+2b+c＜0；④若（﹣5，y1），（，y2）是抛物线上两点，则y1＞y2．

其中说法正确的是（　　）

A. ①② B. ②③ C. ①②④ D. ②③④

【题目】已知百合酒店的三人间和双人间客房标价为：三人间为每人每天200元，双人间为每人每天300元，为吸引客源，促进旅游，在“十一”黄金周期间酒店进行优惠大酬宾，凡团体入住一律五折优惠.一个50人的旅游团在十月二号到该酒店住宿，租住了一些三人间、双人间客房．

（1）如果租住的每个客房正好住满，并且一天一共花去住宿费6300元.求租住了三人间、双人间客房各多少间？

（2）设三人间共住了x人，这个团一天一共花去住宿费y元，请写出y与x的函数关系式；

（3）一天6300元的住宿费是否为最低？如果不是，请设计一种方案：要求租住的房间正好被住满的，并使住宿费用最低，请写出设计方案，并求出最低的费用．

试题分类