题目内容
如图,已知在△ABC中,PR⊥AB于R,PS⊥AC于S,PR=PS,∠1=∠2,则四个结论:①AR=AS;②PQ∥AB;③△BPR≌△CPS;④BP=CP中( )
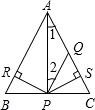
A.全部正确 B.仅①②正确 C.仅①正确 D.仅①④正确
B【考点】全等三角形的判定与性质.
【分析】证RT△APR≌RT△APS,可得AS=AR,∠BAP=∠1,再根据∠1=∠2即可求得QP∥AB,即可解题.
【解答】解:∵在Rt△APR和Rt△APS中,
 ,
,
∴Rt△APR≌Rt△APS,(HL)
∴∠AR=AS,①正确,
∠BAP=∠1,
∵∠1=∠2,
∴∠BAP=∠2,
∴QP∥AB,②正确,
∵△BRP和△QSP中,只有一个条件PR=PS,再没有其余条件可以证明△BRP≌△QSP,故③④错误;
故选B.
【点评】本题考查了全等三角形的判定,考查了全等三角形 对应边、对应角相等的性质,本题中求证RT△APR≌RT△APS是解题的关键.
对应边、对应角相等的性质,本题中求证RT△APR≌RT△APS是解题的关键.

练习册系列答案
相关题目


 D.﹣
D.﹣