题目内容
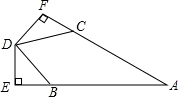
已知,如图,AB=AC,BD=CD,DE⊥AB于点E,DF⊥AC于点F,
(1)求证:DE=DF.
(2)连接BC,求证:线段AD垂直平分线段BC.
【考点】全等三角形的判定与性质;线段垂直平分线的性质.
【专题】证明题.
【分析】(1)连接AD,易证△ACD≌△ABD,根据全等三角形对应角相等的性质可得∠EAD=∠FAD,根据角平分线的性质,即可解答;
(2)由△ACD≌△ABD(已证),得到DC=DB,所以点D在线段BC的垂直平分线上.又AB=AC,所以点A在线段BC的垂直平分线上,即可解答.
【解答】解:(1)如图,连接AD.
在△ACD和△ABD中,
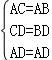
∴△ACD≌△ABD(SSS).
∴∠FAD=∠EAD,
即AD平分∠EAF.
又∵DE⊥AE,DF⊥AF,
∴DE=DF.
(2)∵△ACD≌△ABD(已证).
∴DC=DB,
∴点D在线段BC的垂直平分线上.
又∵AB=AC
∴点A在线段BC的垂直平分线上.
∵两点确定一条直线,
∴AD垂直平分BC.
【点评】本题考查了全等三角形的性质与判定,角平分线的性质、垂直平分线的性质,解决本题的关键是证明△ACD≌△ABD.

练习册系列答案
相关题目
 中的x和y都扩大10倍,那么分式的值 ( )
中的x和y都扩大10倍,那么分式的值 ( ) D.不变
D.不变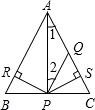

 的系数为﹣2;
的系数为﹣2; 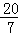 ,0,﹣(﹣3),2.10010001…,42,﹣2π,﹣10,
,0,﹣(﹣3),2.10010001…,42,﹣2π,﹣10,