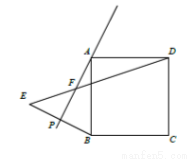
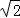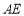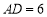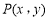题目内容
在正方形 外侧作直线
外侧作直线 ,点
,点 关于直线
关于直线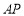 的对称点为
的对称点为 ,连接
,连接 ,其中
,其中 交直线
交直线 于点
于点 .
.
(1)依题意补全图1;
(2)若 ,求
,求 的度数;
的度数;
(3)如图2,若 ,用等式表示线段
,用等式表示线段 之间的数量关系,并证明.
之间的数量关系,并证明.


(1)见解析图形
∠ADF=25°
EF2+FD2=2AB2 证明见解析
【解析】
试题分析:(1)按照题意补全图形
应用轴对称的性质及正方形的性质、等腰三角形的性质解决问题
依照题意画出图形,然后应用轴对称的性质等进行解答
试题解析:(1)补全图形如图所示:
(2)
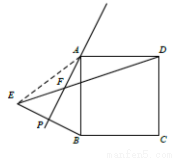
连接AE
则∠PAB=∠PAE=20°,AE=AB=AD
∵ABCD是正方形
∴∠BAD=90°
∴∠EAD=130°
∴∠ADF=25°
(3)
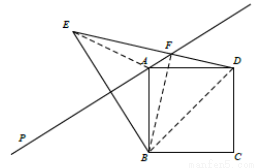
连接AE、BF、BD
由轴对称的性质可得:EF=BF,AE=AB=AD,∠ABF=∠AEF=∠ADF
∴∠BFD=∠BAD=90°
∴BF2+FD2=BD2
∴EF2+FD2=2AB2
考点:1、轴对称的性质;2、正方形的性质;3、勾股定理

练习册系列答案
相关题目