题目内容
6．
如图，在Rt△ABC中，∠C=90°，AB=10，sinA=$\frac{3}{5}$，求BC的长．
分析 利用锐角三角函数的定义和勾股定理进行解答．
解答 解：如图，∵在Rt△ABC中，∠C=90°，AB=10，sinA=$\frac{3}{5}$，
∴$\frac{BC}{AC}$=$\frac{3}{5}$，
则AC=$\frac{5}{3}$BC．
又由勾股定理得到：AB2+BC2=AC2，即102+BC2=$\frac{25}{9}$BC2，
∴BC=7.5．
点评 本题考查了解直角三角形．需要学生掌握锐角三角函数的概念解直角三角形问题．
练习册系列答案
相关题目
如图，边长为1的正方形ABCD，沿着数轴顺时针滚动．起点A和-2重合，则数轴上2016所对应的点是C点．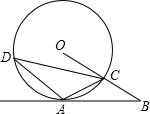
已知：如图A是⊙O上一点，半径OC的延长线与过点A的直线交于B点，OC=BC，∠B=30°．