ΧβΡΩΡΎ»ί
 ‘ΡΕΝ≤ΡΝœΘΚάΐΘΚΥΒΟς¥ζ ΐ Ϋ
‘ΡΕΝ≤ΡΝœΘΚάΐΘΚΥΒΟς¥ζ ΐ Ϋ| x2+1 |
| (x-3)2+4 |
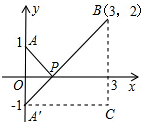
ΫβΘΚ»γΆΦΘ§Ϋ®ΝΔΤΫΟφ÷±Ϋ«Ήχ±ξœΒΘ§ΒψPΘ®xΘ§0Θ© «x÷α…œ“ΜΒψΘ§‘ρ
| x-0)2+12 |
| (x-3)2+22 |
Θ®1Θ©¥ζ ΐ Ϋ
| x2+49 |
| (x-1)2+1 |
Θ®2Θ©«σ¥ζ ΐ Ϋ
| (x-1)2+1 |
| (x-5)2+9 |
ΩΦΒψΘΚΤΫΟφ’ΙΩΣ-ΉνΕΧ¬ΖΨΕΈ Χβ,Ήχ±ξ”κΆΦ–Έ–‘÷
Ή®ΧβΘΚ‘ΡΕΝ–Ά
Ζ÷ΈωΘΚΘ®1Θ©÷±Ϋ”ΗυΨίΧβ“βΩ…ΒΟ≥ωBΒψΉχ±ξΘΜ
Θ®2Θ©άϊ”Ο“―÷ΣΫχΕχΜ≠≥ωΆΦ–ΈΫαΚœ¥ζ ΐ Ϋ
+
ΒΡΉν–Γ÷ΒΈΣPA+PBΒΡ÷ΒΘ§άϊ”ΟΙ¥Ι…Ε®άμΒΟ≥ωΦ¥Ω…Θ°
Θ®2Θ©άϊ”Ο“―÷ΣΫχΕχΜ≠≥ωΆΦ–ΈΫαΚœ¥ζ ΐ Ϋ
| (x-1)2+1 |
| (x-5)2+9 |
Ϋβ¥πΘΚΫβΘΚΘ®1Θ©ΓΏ
Ω…“‘Ω¥≥…ΒψP”κΒψBΘ®3Θ§2Θ©ΒΡΨύάκΘ§
Γύ¥ζ ΐ Ϋ
+
ΒΡ÷ΒΩ…“‘Ω¥≥…ΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–ΒψPΘ®xΘ§0Θ©”κΒψAΘ®1Θ§1Θ©ΓΔΒψBΘ®0Θ§7Θ©ΒΡΨύάκ÷°ΚΆΘ°
Ι ¥πΑΗΈΣΘΚΘ®0Θ§7Θ©ΘΜ
Θ®2Θ©”…Χβ“βΩ…ΒΟΘΚ»γΆΦΘ§Ϋ®ΝΔΤΫΟφ÷±Ϋ«Ήχ±ξœΒΘ§ΒψPΘ®xΘ§0Θ© «x÷α…œ“ΜΒψΘ§‘ρ
Ω…“‘Ω¥≥…ΒψP”κΒψAΘ®1Θ§1Θ©ΒΡΨύάκΘ§
Ω…“‘Ω¥≥…ΒψP”κΒψBΘ®5Θ§3Θ©ΒΡΨύάκΘ§Υυ“‘‘≠¥ζ ΐ ΫΒΡ÷ΒΩ…“‘Ω¥≥…œΏΕΈPA”κPB≥ΛΕ»÷°ΚΆΘ§ΥϋΒΡΉν–Γ÷ΒΨΆ «PA+PBΒΡΉν–Γ÷ΒΦ¥ΈΣΘΚ
=2
Θ°

| (x-3)2+22 |
Γύ¥ζ ΐ Ϋ
| x2+49 |
| (x-1)2+1 |
Ι ¥πΑΗΈΣΘΚΘ®0Θ§7Θ©ΘΜ
Θ®2Θ©”…Χβ“βΩ…ΒΟΘΚ»γΆΦΘ§Ϋ®ΝΔΤΫΟφ÷±Ϋ«Ήχ±ξœΒΘ§ΒψPΘ®xΘ§0Θ© «x÷α…œ“ΜΒψΘ§‘ρ
| (x-1)2+1 |
| (x-5)2+32 |
| 22+62 |
| 10 |

ΒψΤάΘΚ¥ΥΧβ÷ς“ΣΩΦ≤ιΝΥΙ¥Ι…Ε®άμ“‘ΦΑΤΫΟφ’ΙΩΣΆΦΉνΕΧ¬ΖΨΕΈ ΧβΘ§άϊ”Ο ΐ–ΈΫαΚœΒΟ≥ω «ΫβΧβΙΊΦϋΘ°

ΝΖœΑ≤αœΒΝ–¥πΑΗ
 ‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
œύΙΊΧβΡΩ
ΫϋΥΤ ΐ98.76ΆρΨΪ»ΖΒΫΘ®ΓΓΓΓΘ©
| AΓΔΑΌΖ÷ΈΜ | BΓΔΑΌΈΜ | CΓΔ«ßΈΜ | DΓΔΆρΈΜ |
œ¬Ν–‘ΥΥψ’ΐ»ΖΒΡ «Θ®ΓΓΓΓΘ©
| AΓΔx2•x3=x5 |
| BΓΔx2+x2=2x4 |
| CΓΔΘ®-2x2Θ©4=16x6 |
| DΓΔΘ®x+3yΘ©Θ®x-3yΘ©=x2-3y2 |
‘Ύ ΐ÷α…œ”κ-3Ψύάκ4ΗωΒΞΈΜΒΡΒψ±μ ΨΒΡ ΐ «Θ®ΓΓΓΓΘ©
| AΓΔ-1 | BΓΔ-1ΚΆ7 |
| CΓΔ1 | DΓΔ1ΚΆ-7 |
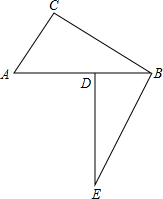 »γΆΦΘΚACΓΆBCΘ§EDΓΆBDΘ§BEΓΆBCΘ§¥ΙΉψΖ÷±πΈΣCΓΔDΓΔBΘ§AB=BEΘ§ ‘ΧΫΨΩBE”κAC+AD÷°ΦδΒΡΙΊœΒΘ°
»γΆΦΘΚACΓΆBCΘ§EDΓΆBDΘ§BEΓΆBCΘ§¥ΙΉψΖ÷±πΈΣCΓΔDΓΔBΘ§AB=BEΘ§ ‘ΧΫΨΩBE”κAC+AD÷°ΦδΒΡΙΊœΒΘ°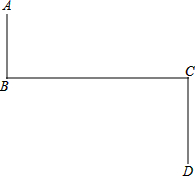 »γΆΦΘ§ABΓΆBCΘ§CDΓΆBCΘ§AB=2Θ§CD=3Θ§BC=7Θ§‘ΎBC…œ«σ“ΜΒψMΘ§Β±BMΒ»”ΎΕύ…Ό ±Θ§ΓςABMΓΉΓςCDMΘΩ
»γΆΦΘ§ABΓΆBCΘ§CDΓΆBCΘ§AB=2Θ§CD=3Θ§BC=7Θ§‘ΎBC…œ«σ“ΜΒψMΘ§Β±BMΒ»”ΎΕύ…Ό ±Θ§ΓςABMΓΉΓςCDMΘΩ