题目内容
 如图,PA、PB是⊙O的切线,A、B是切点,∠AOB=100°,则∠APB=
如图,PA、PB是⊙O的切线,A、B是切点,∠AOB=100°,则∠APB=考点:切线的性质
专题:
分析:根据切线的性质得出∠PAO=∠PBO=90°,根据四边形的内角和定理求出即可.
解答:解:∵PA、PB是⊙O的切线,A、B是切点,
∴∠PAO=∠PBO=90°,
∵∠AOB=100°,
∴∠APB=360°-90°-90°-100°=80°,
故答案为:80.
∴∠PAO=∠PBO=90°,
∵∠AOB=100°,
∴∠APB=360°-90°-90°-100°=80°,
故答案为:80.
点评:本题考查了切线的性质的应用,注意:圆的切线垂直于过切点的半径.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
下列四种标志图案中,既是轴对称图形又是中心对称图形的是( )
A、 中国移动 |
B、 中国联通 |
C、 中国网通 |
D、 中国电信 |
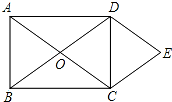 如图,O为矩形ABCD的对角线的交点,DE∥AC,CE∥BD.
如图,O为矩形ABCD的对角线的交点,DE∥AC,CE∥BD. 如图,平行四边形ABCD,E是AB延长线上一点,DE交BC于点F,若BE:AB=2:3,S△BEF=4,则S△CDF=
如图,平行四边形ABCD,E是AB延长线上一点,DE交BC于点F,若BE:AB=2:3,S△BEF=4,则S△CDF=