题目内容
如图，⊙O中∠B=11°，∠C=31°，则∠BOC=________°．
84
分析：首先连接OA，由等腰三角形的性质，易求得∠BAC的度数，又由圆周角定理，即可求得答案．
解答：
解：连接OA，
∵OA=OB=OC，∠B=11°，∠C=31°，
∴∠OAB=∠B=11°，∠OAC=∠C=31°，
∴∠BAC=∠OAB+∠OAC=42°，
∴∠BOC=2∠BAC=84°．
故答案为：84．
点评：此题考查了圆周角定理与等腰三角形的性质．此题难度不大，注意掌握辅助线的作法，注意数形结合思想的应用．
分析：首先连接OA，由等腰三角形的性质，易求得∠BAC的度数，又由圆周角定理，即可求得答案．
解答：
解：连接OA，∵OA=OB=OC，∠B=11°，∠C=31°，
∴∠OAB=∠B=11°，∠OAC=∠C=31°，
∴∠BAC=∠OAB+∠OAC=42°，
∴∠BOC=2∠BAC=84°．
故答案为：84．
点评：此题考查了圆周角定理与等腰三角形的性质．此题难度不大，注意掌握辅助线的作法，注意数形结合思想的应用．
练习册系列答案
相关题目
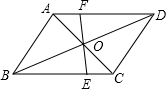如图，?ABCD中，AB⊥AC，AB=1，BC=| 5 |
| A、当∠AOF=90°时，四边形ABEF一定为平行四边形 | ||||
B、当四边形ABEF为直角梯形时，线段EF=
| ||||
| C、当∠AOF=45°时，四边形BEDF一定为菱形 | ||||
| D、在旋转的过程中，线段AF与EC总相等 |
如图，?ABCD中，AB=9，对角线AC与BD相交于点O，AC=12，BD=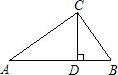
如图在△ABC中，∠ACB=90°，CD⊥AB于D，AC=4，BC=3，则cos∠DCB=
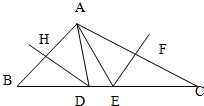14、如图，△ABC中，BC=10，DH为AB的中垂线，EF垂直平分AC，则△ADE的周长是（ ）
20、画出如图所示中立体图形的三视图．