题目内容
4.求方程x2-2x-4=0的满足条件$\left\{\begin{array}{l}{x+1<3x-3}\\{\frac{1}{2}(x-4)<\frac{1}{3}(x-4)}\end{array}\right.$的根.分析 方程利用配方法求出解,再求出不等式组的解集,判断即可.
解答 解:$\left\{\begin{array}{l}{x+1<3x-3①}\\{\frac{1}{2}(x-4)<\frac{1}{3}(x-4)②}\end{array}\right.$,
由①得:x>2;
由②得:x<4,
∴不等式组的解集为2<x<4,
方程整理得:x2-2x=4,
配方得:x2-2x+1=5,即(x-1)2=5,
开方得:x-1=±$\sqrt{5}$,
解得:x1=1+$\sqrt{5}$,x2=1-$\sqrt{5}$,
则方程满足不等式组的根为1+$\sqrt{5}$.
点评 此题考查了解一元二次方程-配方法,以及解一元一次不等式组,熟练掌握完全平方公式是解本题的关键.

练习册系列答案
相关题目
16.方程$\frac{2x}{x-1}$=1+$\frac{1}{x-1}$的解是( )
| A. | x=-1 | B. | x=0 | C. | x=1 | D. | x=2 |
13.下列说法中,正确的是( )
| A. | x=5是方程x+5=0的解 | B. | y=5是3y+15=0的解 | ||
| C. | z=-1是-$\frac{z}{4}$=4的解 | D. | x=0.04是方程25x=1的解 |
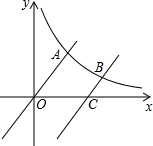 如图,已知函数y=x与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点A,将y=x的图象向下平移6个单位后与双曲线y=$\frac{k}{x}$交于点B,与x轴交于点C.
如图,已知函数y=x与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点A,将y=x的图象向下平移6个单位后与双曲线y=$\frac{k}{x}$交于点B,与x轴交于点C.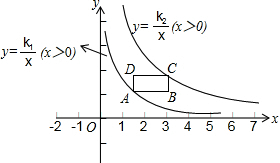 如图,在平面直角坐标系的第一象限中,有一各边所在直线均平行于坐标轴的矩形ABCD,且点A在反比例函数L1:y=$\frac{{k}_{1}}{x}$(x>0)的图象上,点C在反比例函数L2:y=$\frac{{k}_{2}}{x}$(x>0)的图象上.
如图,在平面直角坐标系的第一象限中,有一各边所在直线均平行于坐标轴的矩形ABCD,且点A在反比例函数L1:y=$\frac{{k}_{1}}{x}$(x>0)的图象上,点C在反比例函数L2:y=$\frac{{k}_{2}}{x}$(x>0)的图象上. 如图,已知四边形ABCD以及点O.
如图,已知四边形ABCD以及点O.