题目内容
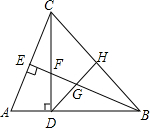 如图,在△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,H是BC边的中点,连结DH、BE与相交于点G,以下结论中正确的结论有( )
如图,在△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,H是BC边的中点,连结DH、BE与相交于点G,以下结论中正确的结论有( )(1)△ABC是等腰三角形 (2)BF=AC
(3)BH:BD:BC=1:
| 2 |
| 3 |
| A、1个 | B、2个 | C、3个 | D、4个 |
考点:全等三角形的判定与性质,等腰三角形的判定与性质,勾股定理
专题:
分析:(1)根据角平分线的定义可得∠ABE=∠CBE,根据等角的余角相等求出∠A=∠BCA,再根据等角对等边可得AB=BC,从而得证;
(2)根据三角形的内角和定理求出∠A=∠DFB,推出BD=DC,根据AAS证出△BDF≌△CDA即可;
(3)根据等腰直角三角形斜边上的中线等于斜边的一半进行解答;
(4)由(2)得出BF=AC,再由BF平分∠DBC和BE⊥AC通过ASA证得△ABE≌△CBE,即得CE=AE=
AC,连接CG,由H是BC边的中点和等腰直角三角形△DBC得出BG=CG,再由直角△CEG得出CG2=CE2+GE2,从而得出CE,GE,BG的关系.
(2)根据三角形的内角和定理求出∠A=∠DFB,推出BD=DC,根据AAS证出△BDF≌△CDA即可;
(3)根据等腰直角三角形斜边上的中线等于斜边的一半进行解答;
(4)由(2)得出BF=AC,再由BF平分∠DBC和BE⊥AC通过ASA证得△ABE≌△CBE,即得CE=AE=
| 1 |
| 2 |
解答:解:(1)∵BE平分∠ABC,
∴∠ABE=∠CBE,
∵CD⊥AB,
∴∠ABE+∠A=90°,∠CBE+∠ACB=90°,
∴∠A=∠BCA,
∴AB=BC,
∴△ABC是等腰三角形;
故(1)正确;
(2)∵CD⊥AB,BE⊥AC,
∴∠BDC=∠ADC=∠AEB=90°,
∴∠A+∠ABE=90°,∠ABE+∠DFB=90°,
∴∠A=∠DFB,
∵∠ABC=45°,∠BDC=90°,
∴∠DCB=90°-45°=45°=∠DBC,
∴BD=DC,
在△BDF和△CDA中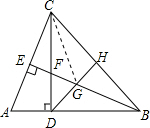
,
∴△BDF≌△CDA(AAS),
∴BF=AC;
故(2)正确;
(3)∵在△BCD中,∠CDB=90°,∠DBC=45°,
∴∠DCB=45°,
∴BD=CD,BC=
BD.
由点H是BC的中点,
∴DH=BH=CH=
BC,
∴BD=
BH,
∴BH:BD:BC=BH:
BH:2BH=1:
:2.
故(3)错误;
(4)由(2)知:BF=AC,
∵BF平分∠DBC,
∴∠ABE=∠CBE,
又∵BE⊥AC,
∴∠AEB=∠CEB,
在△ABE与△CBE中,
,
∴△ABE≌△CBE(AAS),
∴CE=AE=
AC,
∴CE=
AC=
BF;
连接CG.
∵BD=CD,H是BC边的中点,
∴DH是BC的中垂线,
∴BG=CG,
在Rt△CGE中有:CG2=CE2+GE2,
∴CE2+GE2=BG2.
故(4)正确.
综上所述,正确的结论由3个.
故选:C.
∴∠ABE=∠CBE,
∵CD⊥AB,
∴∠ABE+∠A=90°,∠CBE+∠ACB=90°,
∴∠A=∠BCA,
∴AB=BC,
∴△ABC是等腰三角形;
故(1)正确;
(2)∵CD⊥AB,BE⊥AC,
∴∠BDC=∠ADC=∠AEB=90°,
∴∠A+∠ABE=90°,∠ABE+∠DFB=90°,
∴∠A=∠DFB,
∵∠ABC=45°,∠BDC=90°,
∴∠DCB=90°-45°=45°=∠DBC,
∴BD=DC,
在△BDF和△CDA中

|
∴△BDF≌△CDA(AAS),
∴BF=AC;
故(2)正确;
(3)∵在△BCD中,∠CDB=90°,∠DBC=45°,
∴∠DCB=45°,
∴BD=CD,BC=
| 2 |
由点H是BC的中点,
∴DH=BH=CH=
| 1 |
| 2 |
∴BD=
| 2 |
∴BH:BD:BC=BH:
| 2 |
| 2 |
故(3)错误;
(4)由(2)知:BF=AC,
∵BF平分∠DBC,
∴∠ABE=∠CBE,
又∵BE⊥AC,
∴∠AEB=∠CEB,
在△ABE与△CBE中,
|
∴△ABE≌△CBE(AAS),
∴CE=AE=
| 1 |
| 2 |
∴CE=
| 1 |
| 2 |
| 1 |
| 2 |
连接CG.
∵BD=CD,H是BC边的中点,
∴DH是BC的中垂线,
∴BG=CG,
在Rt△CGE中有:CG2=CE2+GE2,
∴CE2+GE2=BG2.
故(4)正确.
综上所述,正确的结论由3个.
故选:C.
点评:本题考查了全等三角形的判定与性质,等腰直角三角形的判定与性质,直角三角形斜边上的中线等于斜边的一半的性质,平行线的性质,熟练掌握三角形全等的判定方法并作辅助线构造出全等三角形是解题的关键.

练习册系列答案
相关题目
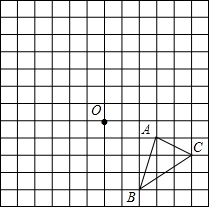 如图,在方格纸中A点的坐标是(3,-1),现将△ABC绕点O逆时针旋转90°得到△A1B1C1,请你作出旋转后的图形,并写出A、B、C三点的对应点的坐标.
如图,在方格纸中A点的坐标是(3,-1),现将△ABC绕点O逆时针旋转90°得到△A1B1C1,请你作出旋转后的图形,并写出A、B、C三点的对应点的坐标. 如图,四边形ABCD的两条对角线相交于点O,AO=CO,BO=DO.求证:AB∥CD.
如图,四边形ABCD的两条对角线相交于点O,AO=CO,BO=DO.求证:AB∥CD.
 如图所给的扇形的半径是12cm,周长是50cm,这个扇形的面积是
如图所给的扇形的半径是12cm,周长是50cm,这个扇形的面积是