题目内容
如图,在△ABC中,以AC为直径作⊙O交BC于点D,交AB于点G,且D是BC中点,DE⊥AB,垂足为E,交AC的延长线于点F.
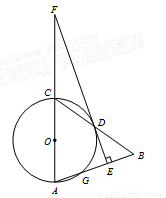
(1)求证:直线EF是⊙O的切线;
(2)CF=5,cos∠A =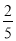 ,求BE的长.[来~源#:*中&教网%]
,求BE的长.[来~源#:*中&教网%]
(1)证明见试题解析;(2)2.
【解析】
试题分析:(1)连结OD.先证明OD是△ABC的中位线,根据中位线的性质得到OD∥AB,再由DE⊥AB,得出OD⊥EF,根据切线的判定即可得出直线EF是⊙O的切线;
(2)先由OD∥AB,得出∠COD=∠A,再解Rt△DOF,根据余弦函数的定义得到cos∠FOD= ,设⊙O的半径为x,解方程
,设⊙O的半径为x,解方程 ,求出
,求出 ,解Rt△AEF,根据余弦函数的定义得到cos∠A=
,解Rt△AEF,根据余弦函数的定义得到cos∠A= ,求出
,求出 ,然后由BE=AB﹣AE即可求解.
,然后由BE=AB﹣AE即可求解.
试题解析:(1)连接CD,∵AO=CO,CD=BD,∴OD //AB,∴∠ODE=∠DEB,∵DE⊥AB,∴∠DEB=90°,∴∠ODE=90°,∴OD⊥BC,∴直线EF是⊙O的切线;

(2)设⊙O的半径为x,则OC=OA=OD,∵OD //AB,∴∠ODC=∠B,∠FOD=∠A,∵OC=OD,∴∠ODC=∠OCD,∴∠B =∠OCD,∴AC=BC=2x,在Rt△ODF中,∠ODF=90°,∴cos∠FOD=cos∠A= ,∴
,∴ ,∴
,∴ ,在Rt△AEF中,∠FEA=90°,∴cos∠A =
,在Rt△AEF中,∠FEA=90°,∴cos∠A = ,∴
,∴ ,∴
,∴ ,∴BE=2.
,∴BE=2.
考点:1.切线的判定;2.解直角三角形.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
 ,则线段HP= .
,则线段HP= .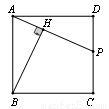

 B.
B. C.
C. D.
D.
 的坐标是( )
的坐标是( )

 件.如果商店计划要每天恰好盈利8000元,并且要使每天的销售量尽量大,求每件商品的售价是多少元.
件.如果商店计划要每天恰好盈利8000元,并且要使每天的销售量尽量大,求每件商品的售价是多少元.