题目内容
已知矩形ABCD中,AB=6cm,AD=8cm,以A为圆心作⊙A,使B,C,D三点中,至少有一个点在圆内,且至少有一个点在圆外,则⊙A的半径r(cm)的取值范围是 .
考点:点与圆的位置关系
专题:
分析:要确定点与圆的位置关系,主要确定点与圆心的距离与半径的大小关系,本题可由勾股定理等性质算出点与圆心的距离d.则d>r时,点在圆外;当d=r时,点在圆上;当d<r时,点在圆内.
解答: 解:如图:
解:如图:
在矩形ABCD中AC=AB
=
=10.
由图可知圆A的半径r的取值范围应大于AD的长,小于对角线AC的长,即6<r<10.
故答案为:6<r<10.
 解:如图:
解:如图:在矩形ABCD中AC=AB
| AB2+AD2 |
| 82+62 |
由图可知圆A的半径r的取值范围应大于AD的长,小于对角线AC的长,即6<r<10.
故答案为:6<r<10.
点评:本题的实质是考查点与圆的位置关系,需要同学们树立数形结合的思想.

练习册系列答案
相关题目
等腰三角形的一个内角为50°,则这个三角形的底角为( )
| A、50°、50° |
| B、80°、80° |
| C、65°、65°或50° |
| D、65°、65° |
某企业今年3月份产值为-2a2月份比3月份减少了10%,5月份比4月份增加了15%,则5月份的产值是( )
| A、(a-10%)(a+15%)万元 |
| B、(1-10%)(1+15%)万元 |
| C、(a-10%+15%)万元 |
| D、a(1-10%+15%)万元 |
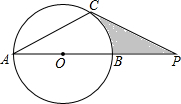 如图,已知:⊙O的直径AB与弦AC的夹角∠A=30°,AC=CP.
如图,已知:⊙O的直径AB与弦AC的夹角∠A=30°,AC=CP. 画出下列三棱柱的三视图.
画出下列三棱柱的三视图.