题目内容
【题目】如图，在△ABC中，∠C=90°，AD平分∠CAB，DE⊥AB于点E，点F是AC上的动点，BD=DF
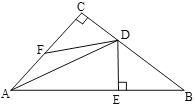
（1）求证：BE=FC；
（2）若∠B=30°，DC=2，此时
，求△ACB的面积．
【答案】（1）证明见解析；（2）6
．
【解析】
（1）根据角平分线的性质可得DC=DE，利用HL可证明△DCF≌△DEB，可得BE=FC；
（2）根据含30°角的直角三角形的性质可求出BD的长，即可求出BC的长，利用三角形面积公式即可得答案．
（1）∵AD平分
，
∴
，
在
和
中，
，
∴
（HL），
∴BE=FC．
（2）AD平分∠BAC，DE⊥AB，∠C=90°，
∴
，
∵∠B=30°，DE⊥AB，
∴BD=2DE=4，
∴BC=CD+BD=6，
∵AC=
，
∴
的面积
．
练习册系列答案
阅读快车系列答案
相关题目
