题目内容
已知直角三角形的两边长a、b满足|a2-4|+
=0,则第三边的长为 .
| b2-5 |
考点:勾股定理,非负数的性质:绝对值,非负数的性质:算术平方根
专题:分类讨论
分析:直接利用绝对值的性质以及二次根式的性质进而得出a2=4,b2=5,再利用分类讨论得出即可.
解答:解:∵直角三角形的两边长a、b满足|a2-4|+
=0,
∴a2=4,b2=5,
∴第三边的长为:
=3或
=1.
故答案为:3或1.
| b2-5 |
∴a2=4,b2=5,
∴第三边的长为:
| 4+5 |
| 5-4 |
故答案为:3或1.
点评:此题主要考查了勾股定理以及非负数的性质,利用分类讨论得出是解题关键.

练习册系列答案
相关题目
已知正比例函数y=(3m+1)x的图象上有两点A(x1,y1)、B(x2,y2),当x1<x2时,有y1>y2,那么m的取值范围是( )
A、m<-
| ||
B、m>-
| ||
| C、m<0 | ||
| D、m>0 |
若(1-2x)4=a0+a1x+a2x2+a3x3+a4x4,那么a1+a2+a3+a4=( )
| A、0 | B、1 | C、2 | D、3 |
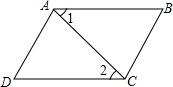 如图,已知∠1=∠2,∠BAD=∠BCD,则下列结论:①AB∥CD;②AD∥BC;③∠D=∠ACB;其中正确的有( )
如图,已知∠1=∠2,∠BAD=∠BCD,则下列结论:①AB∥CD;②AD∥BC;③∠D=∠ACB;其中正确的有( )| A、1个 | B、2个 | C、3个 | D、0个 |
 如图所示的正方形和长方形卡片,拼成一个长为3a+b,宽为a+2b的矩形,需要A类卡片
如图所示的正方形和长方形卡片,拼成一个长为3a+b,宽为a+2b的矩形,需要A类卡片 如图,已知AB∥CD,∠1=35°,BD平分∠ADC,求∠A的度数.
如图,已知AB∥CD,∠1=35°,BD平分∠ADC,求∠A的度数.