题目内容
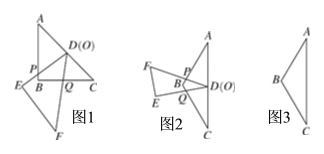
【题目】如图,![]() , 点
, 点![]() 分别在线段
分别在线段![]() 上,且
上,且![]()
![]() 求证:
求证:![]()
![]() 已知
已知![]() 分别是
分别是![]() 的中点,连结
的中点,连结![]()
①若![]() ,求
,求![]() 的度数:
的度数:
②连结![]() 当
当![]() 的长为何值时,四边形
的长为何值时,四边形![]() 是矩形?
是矩形?

【答案】(1)详情见解析;(2)①15°,②![]()
【解析】
(1)通过证明△ABD△ACE进一步求证即可;
(2)①连接AF、AG,利用直角三角形斜边的中线等于斜边的一半求出AF=![]() BD=BF,AG=
BD=BF,AG=![]() CE=GC,由此进一步证明△AFG为等边三角形,最后利用△ABF△ACG进一步求解即可;②连接BC,再连接EF、DG并延长分别交BC于点M、N,首先根据题意求得BM=DE=NC,然后利用△ABC~△AED进一步求解即可.
CE=GC,由此进一步证明△AFG为等边三角形,最后利用△ABF△ACG进一步求解即可;②连接BC,再连接EF、DG并延长分别交BC于点M、N,首先根据题意求得BM=DE=NC,然后利用△ABC~△AED进一步求解即可.
(1)在△ABD与△ACE中,
∵AB=AC,∠A=∠A,AD=AE,
∴△ABD△ACE(SAS),
∴BD=CE;
(2)①连接AF、AG,

∵AF、AG分别为Rt△ABD、Rt△ACE的斜边中线,
∴AF=![]() BD=BF,AG=
BD=BF,AG=![]() CE=GC,
CE=GC,
又∵BD=CE,FG=![]() BD,
BD,
∴AF=AG=FG,
∴△AFG为等边三角形,
易证△ABF△ACG(SSS),
∴∠BAF=∠B=∠C=∠CAG,
∴∠C=15°;
②连接BC、DE,再连接EF、DG并延长分别交BC于点M、N,
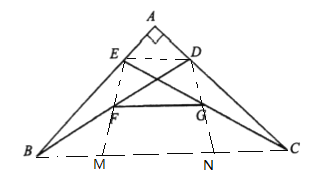
∵△ABC与△AED都是等腰直角三角形,
∴DE∥BC,
∵F、G分别是BD、CE的中点,
∴易证△DEF△BMF,△DEG△NCG(ASA),
∴BM=DE=NC,
若四边形DEFG为矩形,则DE=FG=MN,
∴![]() ,
,
∵DE∥BC,
∴△ABC~△AED,
∴![]() ,
,
∵AC=4,
∴AD=![]() ,
,
∴当AD的长为![]() 时,四边形DEFG为矩形.
时,四边形DEFG为矩形.

 阅读快车系列答案
阅读快车系列答案【题目】某商店分两次购进![]() 、
、![]() 两种商品进行销售,两次购进同一种商品的进价相同,具体情况如下表所示:
两种商品进行销售,两次购进同一种商品的进价相同,具体情况如下表所示:
购进数量(件) | 购进所需费用(元) | ||
|
| ||
第一次 | 30 | 40 | 3800 |
第二次 | 40 | 30 | 3200 |
(1)求![]() 、
、![]() 两种商品每件的进价分别是多少元?
两种商品每件的进价分别是多少元?
(2)商场决定![]() 种商品以每件30元出售,
种商品以每件30元出售,![]() 种商品以每件100元出售.为满足市场需求,需购进
种商品以每件100元出售.为满足市场需求,需购进![]() 、
、![]() 两种商品共1000件,且
两种商品共1000件,且![]() 种商品的数量不少于
种商品的数量不少于![]() 种商品数量的4倍,请你求出获利最大的进货方案,并确定最大利润.
种商品数量的4倍,请你求出获利最大的进货方案,并确定最大利润.