题目内容
已知一条抛物线与y轴的交点为C,顶点为D,直线CD的解析式为y=x+3,并且线段CD的长为 .
.
(1)求这条抛物线的解析式;
(2)设(1)中的抛物线与x轴有两个交点A(x1,0)、B(x2,0),且点A在点B的左侧,求线段AB的长;
(3)若以AB为直径作⊙M,请你判断直线CD与⊙M的位置关系,并说明理由.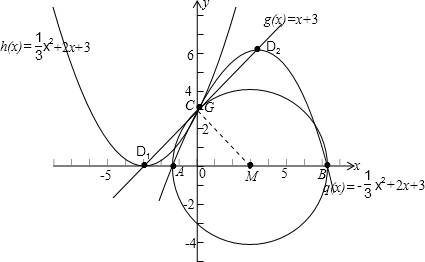
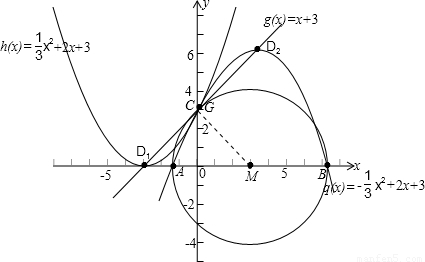
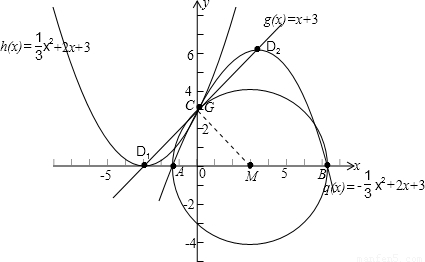
解:(1)由已知可得:C(0,3),D1(-3,0),D2(3,6)…2分
①抛物线过C(0,3),D1(-3,0)时,
设y1=a(x+3)2过(0,3)∴a= …3分
…3分
∴ …4分
…4分
②抛物线过C(0,3),D2(3,6)时
设y2=a(x-3)2+6过(0,3)∴a= …5分
…5分
∴ …6分
…6分
(2)(1)中的抛物线与x轴有两个交点只有②…7分
即
令 得
得
∴A( ,0)、B(
,0)、B( ,0)…8分
,0)…8分
∴|AB|=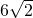 …9分
…9分
(或者不解方程,直接计算|AB|= )
)
(3)直线CD与⊙M相切.…10分
图象及图形如图所示.过M作MG⊥CD于G,
由已知和(2)知M(3,0)∴MG=CD= =
= …11分
…11分
∴直线CD与⊙M相切.…12分
(答案仅参考,若有不同解法,过程和解法都正确,可相应给分)
分析:(1)分类讨论:①抛物线过C(0,3),D1(-3,0)时;②抛物线过C(0,3),D2(3,6)时,利用待定系数法求二次函数的解析式;
(2)利用(1)中的抛物线的图象知:抛物线与x轴有两个交点只有②;然后求得该抛物线与x轴的两个顶点坐标A( ,0)、B(
,0)、B( ,0);最后由两点间的距离公式来求线段AB的长;
,0);最后由两点间的距离公式来求线段AB的长;
(3)直线CD与⊙M相切.过M作MG⊥CD于G.由已知和(2)推知M(3,0),然后根据勾股定理的逆定理证得此结论.
点评:本题考查了二次函数的综合题.解答(1)时,注意要分类讨论,以防漏解.
①抛物线过C(0,3),D1(-3,0)时,
设y1=a(x+3)2过(0,3)∴a=
 …3分
…3分∴
 …4分
…4分②抛物线过C(0,3),D2(3,6)时
设y2=a(x-3)2+6过(0,3)∴a=
 …5分
…5分∴
 …6分
…6分(2)(1)中的抛物线与x轴有两个交点只有②…7分
即

令
 得
得
∴A(
 ,0)、B(
,0)、B( ,0)…8分
,0)…8分∴|AB|=
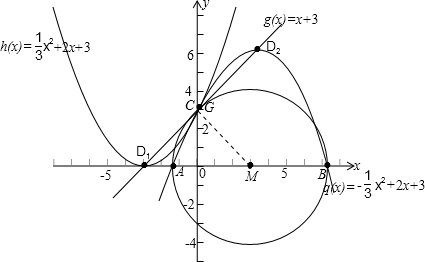
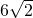 …9分
…9分(或者不解方程,直接计算|AB|=
 )
)(3)直线CD与⊙M相切.…10分
图象及图形如图所示.过M作MG⊥CD于G,
由已知和(2)知M(3,0)∴MG=CD=
 =
= …11分
…11分∴直线CD与⊙M相切.…12分
(答案仅参考,若有不同解法,过程和解法都正确,可相应给分)
分析:(1)分类讨论:①抛物线过C(0,3),D1(-3,0)时;②抛物线过C(0,3),D2(3,6)时,利用待定系数法求二次函数的解析式;
(2)利用(1)中的抛物线的图象知:抛物线与x轴有两个交点只有②;然后求得该抛物线与x轴的两个顶点坐标A(
 ,0)、B(
,0)、B( ,0);最后由两点间的距离公式来求线段AB的长;
,0);最后由两点间的距离公式来求线段AB的长;(3)直线CD与⊙M相切.过M作MG⊥CD于G.由已知和(2)推知M(3,0),然后根据勾股定理的逆定理证得此结论.
点评:本题考查了二次函数的综合题.解答(1)时,注意要分类讨论,以防漏解.

练习册系列答案
相关题目
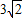 .
.
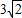 .
.
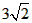 。
。