题目内容
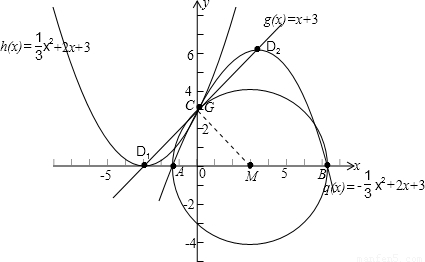
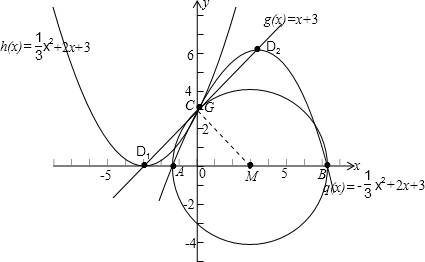
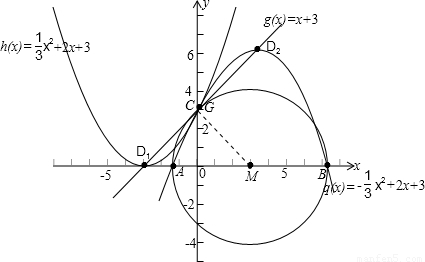
已知一条抛物线与y轴的交点为C,顶点为D,直线CD的解析式为y=x+3,并且线段CD的长为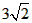 。
。
(1)求这条抛物线的解析式;
(2)设(1)中的抛物线与x轴有两个交点A(x1,0)、B(x2,0),且点A在点B的左侧,求线段AB的长;
(3)若以AB为直径作⊙M,请你判断直线CD与⊙M的位置关系,并说明理由。
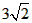 。
。(1)求这条抛物线的解析式;
(2)设(1)中的抛物线与x轴有两个交点A(x1,0)、B(x2,0),且点A在点B的左侧,求线段AB的长;
(3)若以AB为直径作⊙M,请你判断直线CD与⊙M的位置关系,并说明理由。
(1)由题得C(0,3),设顶点D(x,y),∵点D在直线y=x+3上,∴D(x,x+3),得
 解得
解得
 ∴D(3,6)或(-3,0),当D(3,6)时,设抛物线为
∴D(3,6)或(-3,0),当D(3,6)时,设抛物线为

∵抛物线过(0,3)点,∴
当 (-3,0)时,同理可得
(-3,0)时,同理可得
∴所求抛物线为:
(2)∵抛物线与x轴有两个交点,y= 不合题意,舍去。
不合题意,舍去。
抛物线应为: ,
,
令y=0,得 ,
,
解得 ,
,
∵点A在B的左侧,∴A( ,0),B(
,0),B( ,0),
,0),

(3)直线CD与⊙M相切,⊙M的半径 ,M(3,0),
,M(3,0),
设直线y=x+3与x轴交于点E,则E(-3,0),ME=6,
∴OE=OC,
∴∠OEC=45°,
作MG⊥CD于G,则CE=CM,
得 ,
, ,
,
即圆心M到直线CD的距离等于⊙M的半径 ,
,
∴直线CD与⊙M相切
 解得
解得
 ∴D(3,6)或(-3,0),当D(3,6)时,设抛物线为
∴D(3,6)或(-3,0),当D(3,6)时,设抛物线为
∵抛物线过(0,3)点,∴

当
 (-3,0)时,同理可得
(-3,0)时,同理可得
∴所求抛物线为:

(2)∵抛物线与x轴有两个交点,y=
 不合题意,舍去。
不合题意,舍去。抛物线应为:
 ,
,令y=0,得
 ,
,解得
 ,
,∵点A在B的左侧,∴A(
 ,0),B(
,0),B( ,0),
,0),
(3)直线CD与⊙M相切,⊙M的半径
 ,M(3,0),
,M(3,0),设直线y=x+3与x轴交于点E,则E(-3,0),ME=6,
∴OE=OC,
∴∠OEC=45°,
作MG⊥CD于G,则CE=CM,
得
 ,
, ,
,即圆心M到直线CD的距离等于⊙M的半径
 ,
,∴直线CD与⊙M相切

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 .
.
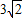 .
.
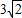 .
.