题目内容
3.如图①,在Rt△ABC中,∠C=90°,AB=10,BC=6,点P从点A出发,沿折线AB-BC向终点C运动,在AB上以每秒5个单位长度的速度运动,在BC上以每秒3个单位长度的速度运动,点Q从点C出发,沿CA方向以每秒$\frac{4}{3}$个单位长度的速度运动,P,Q两点同时出发,当点P停止时,点Q也随之停止.设点P运动的时间为t秒.(1)求线段AQ的长;(用含t的代数式表示)
(2)连结PQ,当PQ与△ABC的一边平行时,求t的值;
(3)如图②,过点P作PE⊥AC于点E,以PE,EQ为邻边作矩形PEQF,点D为AC的中点,连结DF.设矩形PEQF与△ABC重叠部分图形的面积为S.①当点Q在线段CD上运动时,求S与t之间的函数关系式;②直接写出DF将矩形PEQF分成两部分的面积比为1:2时t的值.

分析 (1)利用勾股定理先求出AC,根据AQ=AC-CQ即可解决问题;
(2)分两种情形列出方程求解即可;
(3)①分三种情形a、如图1中,当0≤t≤$\frac{3}{2}$时,重叠部分是四边形PEQF.b、如图2中,当$\frac{3}{2}$<t≤2时,重叠部分是四边形PNQE.C、如图3中,当2<t≤3时,重叠部分是五边形MNPBQ.分别求解即可;
②分两种情形a、如图4中,当DE:DQ=1:2时,DF将矩形PEQF分成两部分的面积比为1:2.b、如图5中,当NE:PN=1:2时,DF将矩形PEQF分成两部分的面积比为1:2.分别列出方程即可解决问题;
解答 解:(1)在Rt△ABC中,∵∠C=90°,AB=10,BC=6,
∴AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=$\sqrt{1{0}^{2}-{6}^{2}}$=8,
∵CQ=$\frac{4}{3}$t,
∴AQ=8-$\frac{4}{3}$t(0≤t≤4).
(2)①当PQ∥BC时,$\frac{AP}{AB}$=$\frac{AQ}{AC}$,
∴$\frac{5t}{10}$=$\frac{8-\frac{4}{3}t}{8}$,
∴t=$\frac{3}{2}$s.
②当PQ∥AB时,$\frac{CQ}{CA}$=$\frac{CP}{CB}$,
∴$\frac{\frac{4}{3}t}{8}$=$\frac{6-3(t-2)}{6}$,
∴t=3,
综上所述,t=$\frac{3}{2}$s或3s时,当PQ与△ABC的一边平行.
(3)①如图1中,a、当0≤t≤$\frac{3}{2}$时,重叠部分是四边形PEQF.
S=PE•EQ=3t•(8-4t-$\frac{4}{3}$t)=-16t2+24t.
b、如图2中,当$\frac{3}{2}$<t≤2时,重叠部分是四边形PNQE.
S=S四边形PEQF-S△PFN=(16t2-24t)-$\frac{1}{2}$•$\frac{4}{5}$[5t-$\frac{5}{4}$(8-$\frac{4}{3}$t)]•$\frac{3}{5}$[5t-$\frac{5}{4}$(8-$\frac{4}{3}$t0]=-$\frac{16}{3}{t}^{2}+40t-48$.
C、如图3中,当2<t≤3时,重叠部分是五边形MNPBQ.
S=S四边形PBQF-S△FNM=$\frac{4}{3}$t•[6-3(t-2)]-$\frac{1}{2}$•[$\frac{4}{3}$t-4(t-2)]•$\frac{3}{4}$[$\frac{4}{3}$t-4(t-2)]=-$\frac{20}{3}$t2+30t-24.
②a、如图4中,当DE:DQ=1:2时,DF将矩形PEQF分成两部分的面积比为1:2.
则有(4-4t):(4-$\frac{4}{3}$t)=1:2,解得t=$\frac{3}{5}$s,
b、如图5中,当NE:PN=1:2时,DF将矩形PEQF分成两部分的面积比为1:2.
∴DE:DQ=NE:FQ=1:3,
∴(4t-4):(4-$\frac{4}{3}$t)=1:3,
解得t=$\frac{6}{5}$s,
综上所述,当t=$\frac{3}{5}$s或$\frac{6}{5}$s时,DF将矩形PEQF分成两部分的面积比为1:2.
点评 本题考查四边形综合题、矩形的性质、勾股定理、相似三角形的性质和判定、平行线分线段成比例定理等知识,解题的关键是学会用分类讨论的思想思考问题,学会构建方程解决问题,属于中考压轴题.

| A. | 若a<0,则$\sqrt{{a}^{2}}$<0 | B. | x实数,且x2=a,则a>0 | ||
| C. | $\sqrt{-x}$有意义时,x≤0 | D. | 0.1的平方根是±0.01 |
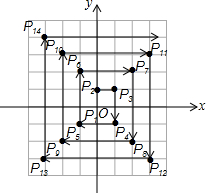 如图,在平面直角坐标系中,每个最小方格的边长均为1个单位长度,P1,P2,P3,…均在格点上,其顺序按图中“→”方向排列,如:P1(0,0),P2(0,1),P3(1,1),P4(1,-1),P5(-1,-1),P6(-1,2)…根据这个规律,点P2017的坐标为( )
如图,在平面直角坐标系中,每个最小方格的边长均为1个单位长度,P1,P2,P3,…均在格点上,其顺序按图中“→”方向排列,如:P1(0,0),P2(0,1),P3(1,1),P4(1,-1),P5(-1,-1),P6(-1,2)…根据这个规律,点P2017的坐标为( )| A. | (-504,-504) | B. | (-505,-504) | C. | (504,-504) | D. | (-504,505) |
 如图所示,该几何体的左视图是( )
如图所示,该几何体的左视图是( )| A. |  | B. |  | C. |  | D. |  |
| A. | 2$\sqrt{3}$+3$\sqrt{3}$=5$\sqrt{6}$ | B. | ($\sqrt{2}+1$)(1-$\sqrt{2}$)=1 | C. | (xy)-1($\frac{1}{2}$xy)2=$\frac{1}{4}$xy | D. | -(-a)4÷a2=a2 |