题目内容
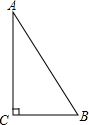已知△ABC中，∠ACB=90°，AC=8，BC=6．在射线BC上取一点D，使得△ABD为等腰三角形，这样的三角形有几个？请你求△ABD的周长．考点：勾股定理,等腰三角形的判定
专题：
分析：分三种情况讨论：①如图1，当AB=AD=10时；如图2，当AB=BD=10时；当AB为底时．
解答：解：在Rt△ABC中，AB=
=10，
①如图1，
当AB=AD=10时，CD=CB=6时，
CD=CB=6，
得△ABD的周长为32m．
②如图2，
当AB=BD=10时，
得CD=4，
在Rt△ACD中，AD=
=
=4
∴△ABD的周长为（20+4
）m．
③如图3，
当AB为底时，设AD=BD=x，则CD=x-6，
在Rt△ACD中，AD2=CD2+AC2，
即x2=（x-6）2+82，解得：x=
，
则△ABD的周长为
m．
| AC2+BC2 |
①如图1，
当AB=AD=10时，CD=CB=6时，
CD=CB=6，
得△ABD的周长为32m．
②如图2，
当AB=BD=10时，
得CD=4，
在Rt△ACD中，AD=
| AC2+CD2 |
| 82+42 |
| 5 |
∴△ABD的周长为（20+4
| 5 |
③如图3，
当AB为底时，设AD=BD=x，则CD=x-6，
在Rt△ACD中，AD2=CD2+AC2，
即x2=（x-6）2+82，解得：x=
| 25 |
| 3 |
则△ABD的周长为
| 80 |
| 3 |
点评：本题考查了勾股定理，解决本题的关键是正确认识到需要讨论，讨论等腰三角形的边应如何分类．
练习册系列答案
相关题目
4a-a的计算结果是（ ）
| A、3 | B、3a | C、4 | D、4a |
下列说法不正确的是（ ）
| A、近似数4.50和4.5是不一样的 |
| B、近似数6.0精确到十分位 |
| C、近似数7.3万精确到千位 |
| D、近似数2.30×105精确到百分位 |
-5的倒数是（ ）
| A、5 | ||
B、
| ||
C、-
| ||
| D、-5 |
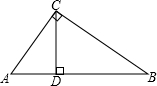在Rt△ABC中，∠C=90°，BC=8，S△ABC=24，求斜边AB上的高．